51 nod 1624 取余最长路 思路：前缀和 + STL（set）二分查找

题目：

写这题花了我一上午时间。

下面是本人（zhangjiuding）的思考过程：

首先想到的是三行，每一行一定要走到。

大概是这样一张图

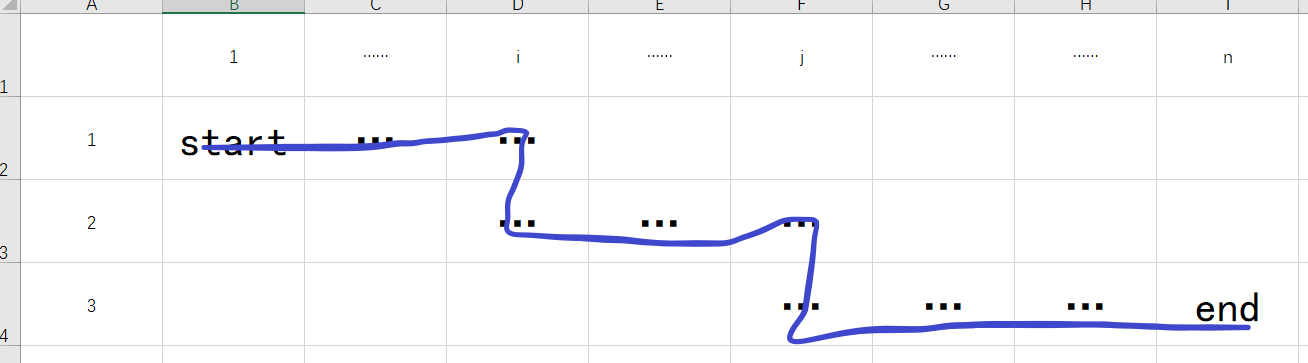
每一行长度最少为1。即第一行(i -1) >= 1，第二行 (j - i) >= 1，第三行 (n - j) >= 1。

我们要求的就是这条路径上的和。

我们发现只要 i 和 j 固定了，结果就固定了。

如果每次都要重新求和的话时间复杂度肯定不够，所以我这个时候想到了前缀和。

用sum[a][b]表示第a行（总共只有3行）前b个数字的和。

第一行可以用 sum[1][i]来表示，第二行可以用sum[2][j]-sum[2][i-1]来表示，第三行可以用sum[3][n]-sum[3][j-1]来表示。

（此处用到了i-1所以我们吧sum[][0]空出来，这样就不会越界）

ans = sum[1][i] + sum[2][j] - sum[2][i-1] + sum[3][n] - sum[3][j-1];

每一组i、j都有一个固定结果，我们求出其中取模最大的那个就好了。

现在求和的问题解决了，该固定i , j 了。

下面看到i的取值范围（1 <= i <= n），j的取值范围（i <= j <= n）

如果遍历i和j的话时间复杂度还是O(n^2)，所以前缀和+暴力肯定是会超时的。

如果能优化一点到O（n*log(n)）就好了，这样就不会超时了。

那么能优化吗？答案是肯定的。

我们先把我们的每一对i，j对应的ans分离一下。

定义up = sum[1][i] - sum[2][i-1];

　　down = sum[2][j] + sum[3][n] - sum[3][j-1];

这样up中只含有i，down中只含有j。

因为我们知道结果只和 i , j 有关，

如果我们能把每一个up可能的down存起来，二分法找出那个能让结果最大的down值，然后用up+down更新ans就好了。

这样时间复杂度就只有O(n*log(n))了。

你可能看到这里还有疑问，先怀着疑问，后面我会把我碰到的问题和疑问都讲出来。

先看代码有助于理解：

#include <bits\stdc++.h>
using namespace std;
typedef long long ll;

//定义结构体，value存输入的值，sum存当前行的前缀和。
struct node{
    ll value;ll sum;
}a[][];
//ifstream in("in15.txt");

int main(){
    int n;
    ll p;
    cin >> n >> p;
    for(int i = ;i <= ; i++){
        for(int j = ;j <= n; j++){
            cin >> a[i][j].value;
            a[i][j].sum = a[i][j].value+a[i][j-].sum;   // 求前缀和。
        }
    }

    ll ans = ;
    set<ll> s;   // 用set存当前i值可能碰到的j值对应的down。
    set<ll>::iterator it;

    //反向遍历是因为down的范围可以慢慢扩张，不用删除set中的元素
    for(int i = n; i >= ; i--){
        ll up = (a[][i].sum-a[][i-].sum)%p;   //  当前i值对应的up。
        up = (up+p)%p;                      //  强行变成正数。
        ll down = (a[][i].sum+a[][n].sum-a[][i-].sum)%p; // 当前i值对应的down。
        down = (down+p)%p;                  //  强行变成正数。
//        cout << "i:" << i << endl;
//        cout << "up:"<< up << endl;
//        cout << "down:" << down << endl;

        s.insert(down);//因为肯定是j >= i的，所以每次把当前i值对应的down加入到set，set就会表示可能取到的所有的j对应的down的集合。 

        //明确一点，set里装的全是down。 

        // 二分查找，找到一个down值与up相加后最大。
        it = s.lower_bound(p-up);   // 找到第一个大于等于p-up的down值，我们需要将it--，求出第一个比p-up小的。

        //注意，1、2顺序不能变。
        if(it != s.begin()) {   //1.如果等于it = s.begin(),因为it还要减一下，相当于没有找到合适的值。
            it--;                // 2.it--，让it指向第一个比p-up小的值。
            ans = max(ans,(up+*it)%p);  // 更新 ans。
        }

        //可能第一个比p-up小的down值加上up后还是比较小，反而down的最大值加上up后取模还比较大，所以话线性时间更新一下ans。
    it = s.end();
    it--;
    ans = max(ans,(*it+up)%p);
    }
    cout << ans << endl;
    return ;
}
//writed by zhangjiuding

看到这里可能有一个最大的问题，那就是强行变正数的问题。

比如p = 10, up求出来的是-3，而down求出来是6，（-3 + 6）%10 = 3还是正数，强行将up变成正数是否会出错呢？

答案是肯定不会，   up 强行变正后是7，（7+6）% 10 = 3，还是3。

看起来逻辑性并不强，但是我试过了很多组数据都是一样的结果，强行变正并不影响结果。

我的猜测是：因为数组中所有的数都是正数或者0，所以每一个up+down一定会大于0。

　　　　　　如果up小于0，那么它可以取到的所有的down都会使 up+down >= 0。

　　　　　　只是这些值是取过模的，所以会出现负数，我们需要将它放在0~(p-1)之间。