动态规划略有所得 数字三角形(POJ1163)

在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。 三角形的行数大于1小于等于100，数字为 0 - 99

输入格式：

5      //表示三角形的行数    接下来输入三角形

7

3   8

8   1   0

2   7   4   4

4   5   2   6   5

要求输出最大和

用递归解决很简单，从上到下遍历一边。

从第一行第一个开始寻找，判断左下或右下哪一个更大，用缓存数组提高效率

     if (i>=n||j>=n) {
         return 0;
     }
     if (cache[i][j] != -1) {
         return cache[i][j];
     }
     return cache[i][j]=Math.max(maxSum(i+1, j, n), maxSum(i+1,j+1,n))+num[i][j];
     

但是递归的效率很慢，不是一个好方法。

那么动态规划呢。

从下至上，首先计算最底层 。底层是无需计算的，保存即可。

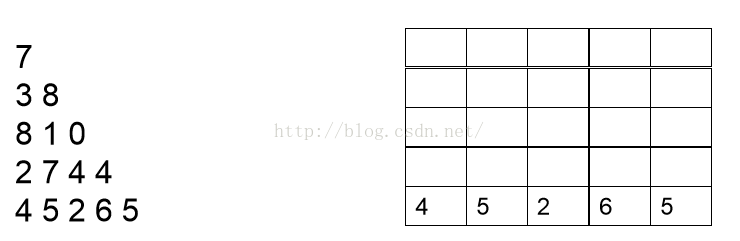
下一步计算倒数第二层。

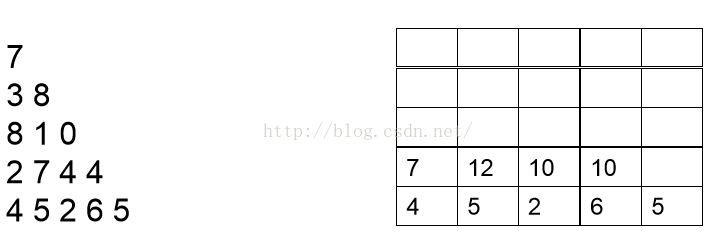
那么用循环就可以很简单的计算出最上面的第一行第一个即为所求

 public class POJ1163 {
     public static void main(String[] args) {
         Scanner sc = new Scanner(System.in);
         int n = sc.nextInt();
         int[][] num = new int[n][n];
         int[][] cache = new int[n][n];
         int i = 0;
         while (i < n) {
             int j = 0;
             while (j <= i) {
                 num[i][j] = sc.nextInt();
                 j++;
             }
             i++;
         }
         for (int j = 0; j < n; j++) {
             Arrays.fill(cache[j], -1);
         }
         long startTime=System.currentTimeMillis();   //获取开始时间
         System.out.println(maxSum(0,0,n,cache,num));
         long endTime=System.currentTimeMillis(); //获取结束时间
         System.out.println("程序运行时间： "+(endTime-startTime)+"ms");

         int[][] cal = new int[n][n];
         startTime=System.currentTimeMillis();   //获取开始时间
         for (i  = 0; i < n; i++) {
             cal[n-1][i] = num[n-1][i]; //保存最后一行就可以了
         }
         for ( i = n-2; i >= 0; i--) {
             for (int j = 0; j <= i; j++) {
                 cal[i][j] = Math.max(cal[i+1][j], cal[i+1][j+1])+num[i][j];
             }
         }
         System.out.println(cal[0][0]);
         endTime=System.currentTimeMillis(); //获取结束时间
         System.out.println("程序运行时间： "+(endTime-startTime)+"ms");

     }
     public static int maxSum(int i,int j, int n, int[][] cache,int [][] num) {
         if (i>=n||j>=n) {
             return 0;
         }
         if (cache[i][j] != -1) {
             return cache[i][j];
         }
         return cache[i][j]=Math.max(maxSum(i+1, j, n,cache,num), maxSum(i+1, j+1,n,cache,num))+num[i][j];
     }

 }

还有一种节省空间的方法 用一维数组保存最大值

     int[] cal1 = new int[n];
     for (i  = 0; i < n; i++) {
         cal1[i] = num[n-1][i]; //sikao
     }
     for ( i = n-2; i >= 0; i--) {
         for (int j = 0; j <= i; j++) {
             cal1[j] = Math.max(cal1[j], cal1[j+1])+num[i][j];
         }
     }

接下来，我们就进行一下总结：

    递归到动规的一般转化方法

递归函数有n个参数，就定义一个n维的数组，数组的下标是递归函数参数的取值范围，数组元素的值是递归函数的返回值，这样就可以从边界值开始， 逐步填充数组，相当于计算递归函数值的逆过程。

    动规解题的一般思路

    1. 将原问题分解为子问题

• 把原问题分解为若干个子问题，子问题和原问题形式相同或类似，只不过规模变小了。子问题都解决，原问题即解决(数字三角形例）。
• 子问题的解一旦求出就会被保存，所以每个子问题只需求 解一次。

    2.确定状态

• 在用动态规划解题时，我们往往将和子问题相关的各个变量的一组取值，称之为一个“状 态”。一个“状态”对应于一个或多个子问题， 所谓某个“状态”下的“值”，就是这个“状 态”所对应的子问题的解。
• 所有“状态”的集合，构成问题的“状态空间”。“状态空间”的大小，与用动态规划解决问题的时间复杂度直接相关。 在数字三角形的例子里，一共有N×(N+1)/2个数字，所以这个问题的状态空间里一共就有N×(N+1)/2个状态。

整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次，且在每个状态上作计算所花的时间都是和N无关的常数。

    3.确定一些初始状态（边界状态）的值

以“数字三角形”为例，初始状态就是底边数字，值就是底边数字值。

    4. 确定状态转移方程

定义出什么是“状态”，以及在该“状态”下的“值”后，就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的 “状态”，求出另一个“状态”的“值”(递推型)。状态的迁移可以用递推公式表示，此递推公式也可被称作“状态转移方程”。

数字三角形的状态转移方程:

    能用动规解决的问题的特点

1) 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的，我们就称该问题具有最优子结 构性质。

2) 无后效性。当前的若干个状态值一旦确定，则此后过程的演变就只和这若干个状态的值有关，和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态，没有关系。