[笔记]RankSVM 和 IR SVM

之前的博客：http://www.cnblogs.com/bentuwuying/p/6681943.html中简单介绍了Learning to Rank的基本原理，也讲到了Learning to Rank的几类常用的方法：pointwise，pairwise，listwise。这篇博客就很多公司在实际中通常使用的pairwise的方法进行介绍，首先我们介绍相对简单的 RankSVM 和 IR SVM。

1. RankSVM

RankSVM的基本思想是，将排序问题转化为pairwise的分类问题，然后使用SVM分类模型进行学习并求解。

1.1 排序问题转化为分类问题

对于一个query-doc pair，我们可以将其用一个feature vector表示：x。而排序函数为f(x)，我们根据f(x)的大小来决定哪个doc排在前面，哪个doc排在后面。即如果f(x_i) > f(x_j)，则x_i应该排在x_j的前面，反之亦然。可以用下面的公式表示：

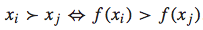
理论上，f(x)可以是任意函数，为了简单起见，我们假设其为线性函数：。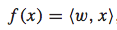

如果这个排序函数f(x)是一个线性函数，那么我们便可以将一个排序问题转化为一个二元分类问题。理由如下：

首先，对于任意两个feature vector x_i和 x_j，在f(x)是线性函数的前提下，下面的关系都是存在的：

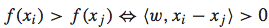
然后，便可以对x_i和 x_j的差值向量考虑二元分类问题。特别地，我们可以对其赋值一个label：

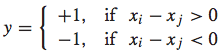
1.2 SVM模型解决排序问题

将排序问题转化为分类问题之后，我们便可以使用常用的分类模型来进行学习，这里我们选择了Linear SVM，同样的，可以通过核函数的方法扩展到 Nonlinear SVM。

如下面左图所示，是一个排序问题的例子，其中有两组query及其相应的召回documents，其中documents的相关程度等级分为三档。而weight vector w对应了排序函数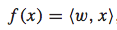，可以对query-doc pair进行打分和排序。

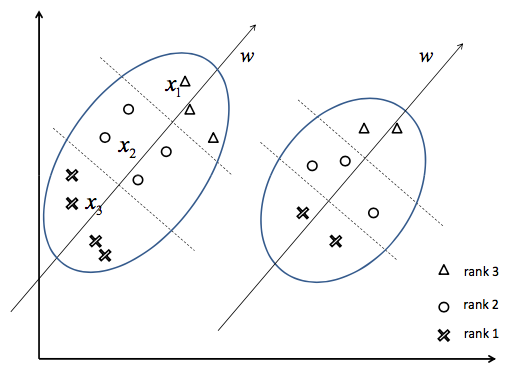
而下面右图则展示了如何将排序问题转化为分类问题。在同一个组内（同一个query下）的不同相关度等级的doc的feature vector可以进行组合，形成新的feature vector：x₁-x₂，x₁-x₃，x₂-x₃。同样的，label也会被重新赋值，例如x₁-x₂，x₁-x₃，x₂-x₃这几个feature vector的label被赋值成分类问题中的positive label。进一步，为了形成一个标准的分类问题，我们还需要有negative samples，这里我们就使用前述的几个新的positive feature vector的反方向向量作为相应的negative samples：x₂-x₁，x₃-x₁，x₃-x₂。另外，需要注意的是，我们在组合形成新的feature vector的时候，不能使用在原始排序问题中处于相同相似度等级的两个feature vector，也不能使用处于不同query下的两个feature vector。

        

1.2 SVM模型的求解过程

转化为了分类问题后，我们便可以使用SVM的通用方式进行求解。首先我们可以得到下面的优化问题：

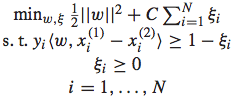
通过将约束条件带入进原始优化问题的松弛变量中，可以进一步转化为非约束的优化问题：

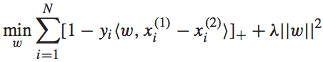
加和的第一项代表了hinge loss，第二项代表了正则项。primal QP problem较难求解，如果使用通用的QP解决方式则费时费力，我们可以将其转化为dual problem，得到一个易于求解的形式：

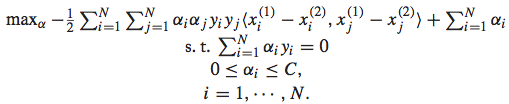
而最终求解得到相应的参数后，排序函数可以表示为：

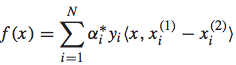
于是，RankSVM方法求解排序问题的步骤总结起来，如下图所示：

2. IR SVM

2.1 loss function的改造

上面介绍的RankSVM的基本思想是，将排序问题转化为pairwise的分类问题，然后使用SVM分类模型进行学习并求解。所以其在学习过程中，是使用了0-1分类损失函数（虽然实际上是用的替换损失函数hinge loss）。而这个损失函数的优化目标跟Information Retrieval的Evaluation常用指标（不仅要求各个doc之间的相对序关系正确，而且尤其重视Top的doc之间的序关系）还是存在gap的。所以有研究人员对此进行了研究，通过对RankSVM中的loss function进行改造从而使得优化目标更好地与Information Retrieval问题的常用评价指标相一致。

首先，我们通过一些例子来说明RankSVM在应用到文本排序的时候遇到的一些问题，如下图所示。

第一个问题就是，直接使用RankSVM的话，会将不同相似度等级的doc同等看待，不会加以区分。这在具体的问题中又会有两种形式：

1）Example 1中，3 vs 2 和 3 vs 1的两个pair，在0-1 loss function中是同等看待的，即它们其中任一对的次序的颠倒对loss function的增加大小是一样的。而这显然是不合理的，因为3 vs 1的次序颠倒显然要比 3 vs 2的次序的颠倒要更加严重，需要给予不同的权重来区分。

2）Example 2中，ranking-1是position 1 vs position 2的两个doc的位置颠倒了，ranking-2是position 3 vs position 4的两个doc的位置颠倒了，这两种情况在0-1 loss function中也是同等看待的。这显然也是不合理的，由于IR问题中对于Top doc尤其重视，ranking-1的问题要比ranking-2的问题更加严重，也是需要给予不同的权重加以区分。

第二个问题是，RankSVM对于不同query下的doc pair同等看待，不会加以区分。而不同query下的doc的数目是很不一样的。如Example 3所示，query-4的doc书目要更多，所以在训练过程中，query-4下的各个doc pair的训练数据对于模型的影响显然要比query-3下的各个doc pair的影响更大，所以最终结果的模型会有bias。

IR SVM针对以上两个问题进行了解决，它使用了cost sensitive classification，而不是0-1 classification，即对通常的hinge loss进行了改造。具体来说，它对来自不同等级的doc pair，或者来自不同query的doc pair，赋予了不同的loss weight：

1）对于Top doc，即相似度等级较高的doc所在的pair，赋予较大的loss weight。

2）对于doc数目较少的query，对其下面的doc pair赋予较大的loss weight。

2.2 IR SVM的求解过程

IR SVM的优化问题可以表示如下：

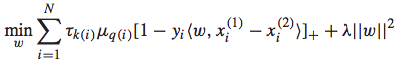
其中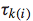，代表了隶属于第k档grade pair的instance的loss weight值。这个值的确定有一个经验式的方法：对隶属于这一档grade pair的两个doc，随机交换它们的排序位置，看对于NDCG@1的减少值，将所有的减少值求平均就得到了这个loss weight。可以想象，这个loss weight值越大，说明这个pair的doc对于整体评价指标的影响较大，所以训练时候的重要程度也相应较大，这种情况一般对应着Top doc，这样做就是使得训练结果尤其重视Top doc的排序位置问题。反之亦然。

而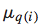这个参数则对应了query的归一化系数。可以表示为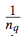，即该query下的doc数目的倒数，这个很好理解，如果这个query下的doc数目较少，则RankSVM训练过程中相对重视程度会较低，这时候通过增加这个权重参数，可以适当提高这个query下的doc pair的重要程度，使得模型训练中能够对不同的query下的doc pair重视程度相当。

IR SVM的优化问题如下：

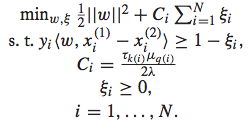
同样地，也需要将其转化为dual problem进行求解：

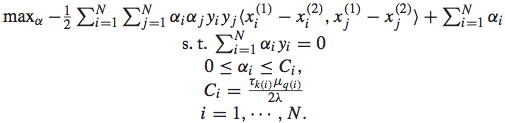
而最终求解得到相应的参数后，排序函数可以表示为：

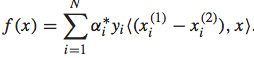
于是，IR SVM方法求解排序问题的步骤总结起来，如下图所示：

版权声明：

本文由笨兔勿应所有，发布于http://www.cnblogs.com/bentuwuying。如果转载，请注明出处，在未经作者同意下将本文用于商业用途，将追究其法律责任。