Coursera 机器学习笔记（三）

主要为第四周、第五周课程内容：神经网络

神经网络模型引入

之前学习的线性回归还是逻辑回归都有个相同缺点就是：特征太多会导致计算量太大。如100个变量，来构建一个非线性模型。即使只采用两两特征组合，都会有接近5000个组成的特征。这对于普通的线性回归和逻辑回归计算特征量太大了。因此，神经网路孕育而生。

神经网络最初产生的目的是制造能模拟大脑的机器，能很好地解决不同的机器学习问题。模型表示为：

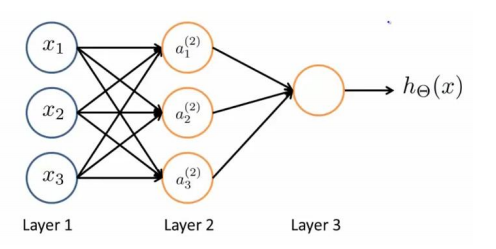
第一层为输入层，最后一层为输出层，中间的层为隐藏层。如把逻辑回归最为神经网络模型的神经元，a(j)I 代表第j层的第i个激活单元，θ(j)表示从第j层映射到第j+1层时的权重矩阵，其尺寸为第j+1层的激活单元数量为行数，第j层的激活单元数+1为列数的矩阵,如θ(1)尺寸为3*4。对于上图所示模型的表达为：

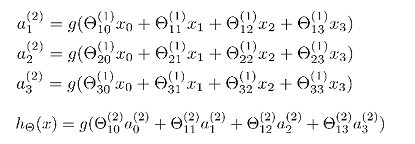
正向传播算法(Forward Propagation)

利用向量化的方法会使计算大为简便。计算上图第二层为例：

这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算，我们需要将训练集特征矩阵进行转置，使得同一个实例的特征都在同一列里。

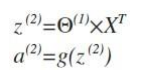
而计算第三层（输出层），可以把第二层看成是输入层，第三层为上述的第二层。

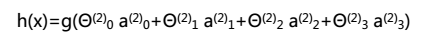
我们可以把 a0,a1,a2,a3看成更为高级的特征值，也就是 x0,x1,x2,x3的进化体，并且它们是由 x 与决定的，因为是梯度下降的，所以 a 是变化的，并且变得越来越厉害，所以这些更高级的特征值远比仅仅将 x 次方厉害，也能更好的预测新数据。

多分类

当我们有不止两种分类时（也就是 y=1,2,3….），比如以下这种情况，该怎么办？如y=4

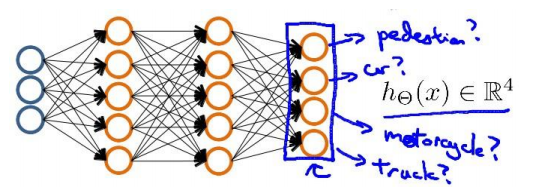
利用one-vs-all思想：神经网络算法的输出结果为四种可能情形之一

代价函数

引入标记表示方法：

• L代表神经网络的层数
• Si代表第i层的处理单元（包括偏见单元）的个数
• SL代表最后一层中的处理单元的个数
• K代表希望分类的个数，与SL相等

逻辑回归中的代价函数为：

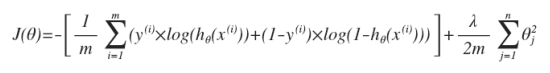
逻辑回归中只有一个输出变量，而在神经网络中有很多输出变量，h(x) 是个一个维度为K的向量，因此因变量也是一个维度为K的向量。神经网络相应的代价函数为：

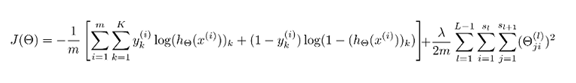
反向传播算法

综合

网络结构：

第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多少个单元。

• 第一层的单元数即我们训练集的特征数量
• 最后一层的单元数是我们训练集的结果的类的数量
• ，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好

我们真正要决定的是隐藏层的层数和每个中间层的单元数。

训练神经网络：

1. 参数的随机初始化
2. 利用正向传播方法计算所有的 hθ(x)
3. 编写计算代价函数 J 的代码
4. 利用反向传播方法计算所有偏导数
5. 利用数值检验方法检验这些偏导数
6. 使用优化算法来最小化代价函数