NOIP2015斗地主[DFS 贪心]

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

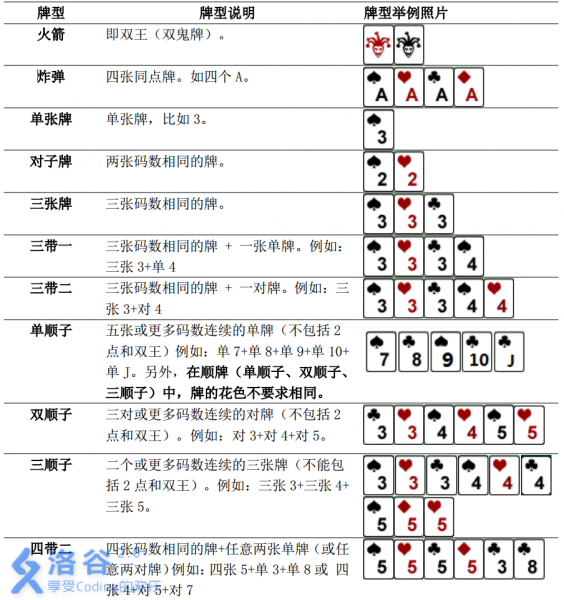
输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为0 1，大王的表示方法为0 2。

输出格式：

共T行，每行一个整数，表示打光第i手牌的最少次数。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

对于不同的测试点，我们约定手牌组数T与张数n的规模如下：

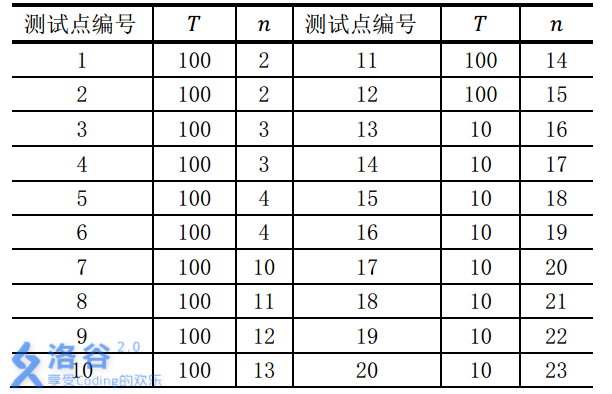
数据保证：所有的手牌都是随机生成的。

题解：

如果不考虑顺子，其他的走法步数可以直接贪心出来

那么搜索顺子的出法就可以了

(PS:数据随机意味着有些情况不考虑也能过)

//

//  main.cpp

//  noip2015斗地主

//

//  Created by Candy on 12/11/2016.

//  Copyright © 2016 Candy. All rights reserved.

//

#include <iostream>

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <cmath>

using namespace std;

typedef long long ll;

const int N=;

inline int read(){

    char c=getchar();int x=,f=;

    while(c<''||c>''){if(c=='-')f=-;c=getchar();}

    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}

    return x*f;

}

int T,n,a[N],t[N],x,b,ans=;

char s[];

int c[];

inline int cal(){

    int cnt=;

    memset(c,,sizeof(c));

    for(int i=;i<=;i++) c[a[i]]++;

    while(c[]&&c[]>=) c[]--,c[]-=,cnt++;

    while(c[]&&c[]>=) c[]--,c[]-=,cnt++;

    while(c[]&&c[]) c[]--,c[]--,cnt++;//for 2 c[4]

    while(c[]&&c[]) c[]--,c[]--,cnt++;

    while(c[]&&c[]) c[]--,c[]--,cnt++;

    return cnt+c[]+c[]+c[]+c[];

}

void dfs(int d){

    if(d>=ans) return;

    ans=min(ans,d+cal());

    for(int i=;i<=;i++){//

        int j=i;

        while(a[j]>=){

            j++;

            if(j-i>=){

                for(int k=i;k<j;k++) a[k]-=;

                dfs(d+);

                for(int k=i;k<j;k++) a[k]+=;

            }

        }

    }

    for(int i=;i<=;i++){

        int j=i;

        while(a[j]>=){

            j++;

            if(j-i>=){

                for(int k=i;k<j;k++) a[k]-=;

                dfs(d+);

                for(int k=i;k<j;k++) a[k]+=;

            }

        }

    }

    for(int i=;i<=;i++){

        int j=i;

        while(a[j]){

            j++;

            if(j-i>=){

                for(int k=i;k<j;k++) a[k]--;

                dfs(d+);

                for(int k=i;k<j;k++) a[k]++;

            }

        }

    }

}

int main(int argc, const char * argv[]) {

    T=read();n=read();

    while(T--){

        memset(a,,sizeof(a));

        for(int i=;i<=n;i++){

            x=read();b=read();

            if(x==) x=;

            else if(x) x--;

            a[x]++;

        }

        ans=;

        dfs();

        printf("%d\n",ans);

    }

    return ;

}