【2020.11.30提高组模拟】剪辣椒(chilli)

剪辣椒（chilli）

题目描述

在花园里劳累了一上午之后，你决定用自己种的干辣椒奖励自己。

你有n个辣椒，这些辣椒用n-1条绳子连接在一起，任意两个辣椒通过用若干个绳子相连，即形成一棵树。

你决定分三餐吃完这些辣椒，因此需要剪断其中两根绳子，从而得到三个组成部分，每一餐吃一个组成部分即可。



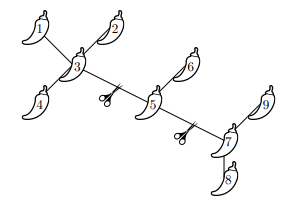
每一餐不可以太辣，所以你会寻找一个剪绳子的方法，使得最大组成部分和最小组成部分的辣椒数量差最小。计算出这个最小差值。

输入格式

输入文件名为chilli.in。

第一行一个整数n，表示辣椒的数量。辣椒从1到n进行编号。

下面n-1行每一行包含两个整数x和y（1≤x，y≤n），表示辣椒x和辣椒y直接用一根绳子相连。

输出格式

输出文件名为chilli.out。

输出最小差值。

题解

题目大意：删掉一棵树上的两条边使得形成的三棵树里\(size\)最大的减\(size\)最小的差值最小，问最小差值

先求出以每个点为根的子树的大小\(size_i\)（假定1为整棵树的根）

然后枚举每个点（用\(dfs\)，在到每个点的时候就计算贡献，即删除当前点与父亲的边，做完之后把\(n-size_x\)加到\(set\)，结束后从\(set\)中移除），删掉它与它父亲的边，这时将整棵树分成两部分：\(size_x\)和\(n-size_x\)，然后在\(n-size_x\)里找到\(\lceil\dfrac{n-size_x}{2}\rceil\)的前驱后继，这里可以用\(set\)里的\(lower\_bound\)（不会用\(set\)可以自行搜索，这里推荐一篇写的比较好的文章https://blog.csdn.net/qq_34243930/article/details/81481929）。关于另一条边，有两种情况，一种是祖先边，上面已经计算，另一种是非祖先边，可以再用一个\(dfs\)，但与上面有所不同，这里是删除当前点与儿子的边，然后结束后加入\(size_x\)

Code

#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#define inf 2147483600
using namespace std;
struct node
{
	int next,to,head;
}a[400001];
int n,x,y,ans,tot,size[200001];
multiset<int> q;
multiset<int>::iterator it;
void add(int x,int y)
{
	a[++tot].to=y;
	a[tot].next=a[x].head;
	a[x].head=tot;
}
void getsize(int now,int fa)
{
	size[now]=1;
	for (int i=a[now].head;i;i=a[i].next)
	{
		if (a[i].to==fa) continue;
		getsize(a[i].to,now);
		size[now]+=size[a[i].to];
	}
}
int getans(int x,int y,int z) {return max(x,max(y,z))-min(x,min(y,z));}
void calc(int x)
{
	int p=n-size[x];
	it=q.lower_bound((p+1)>>1);
	if (it!=q.end()) ans=min(ans,getans(size[x],p-*it,*it));
	if (it!=q.begin()) it--,ans=min(ans,getans(size[x],p-*it,*it));
	it=q.lower_bound(max(size[x],p-size[x]));
	if (it!=q.end()) ans=min(ans,*it*2-p);
}
void dfs1(int now,int fa)
{
	calc(now);
	q.insert(n-size[now]);
	for (int i=a[now].head;i;i=a[i].next)
	{
		if (a[i].to==fa) continue;
		dfs1(a[i].to,now);
	}
	q.erase(n-size[now]);
}
void dfs2(int now,int fa)
{
	for (int i=a[now].head;i;i=a[i].next)
	{
		if (a[i].to==fa) continue;
		calc(a[i].to);
		dfs2(a[i].to,now);
	}
	q.insert(size[now]);
}
int main()
{
	freopen("chilli.in","r",stdin);
	freopen("chilli.out","w",stdout);
	scanf("%d",&n);
	for (int i=1;i<n;++i)
	{
		scanf("%d%d",&x,&y);
		add(x,y);add(y,x);
	}
	ans=inf;
	getsize(1,0);
	dfs1(1,0);
	dfs2(1,0);
	printf("%d\n",ans);
	fclose(stdin);
	fclose(stdout);
	return 0;
}