ALGEBRA-1 向量空间

向量空间对加法封闭 对数乘封闭

直和:表示的唯一性



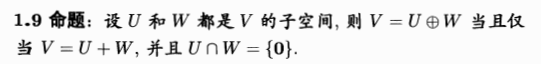
ALGEBRA-1 向量空间的更多相关文章
- 读Linear Algebra -- Gilbert Strang
转眼间我的学士学位修读生涯已经快要到期了,重读线性代数,一是为了重新理解Algebra的的重要概念以祭奠大一刷过的计算题,二是为了将来的学术工作先打下一点点(薄弱的)基础.数学毫无疑问是指导着的科研方 ...
- 【线性代数】3-1:向量空间(Space of Vectors)
title: [线性代数]3-1:向量空间(Space of Vectors) categories: Mathematic Linear Algebra keywords: Vectors Spac ...
- 【线性代数】Linear Algebra Big Picture
Abstract: 通过学习MIT 18.06课程,总结出的线性代数的知识点相互依赖关系,后续博客将会按照相应的依赖关系进行介绍.(2017-08-18 16:28:36) Keywords: Lin ...
- Linear Algebra From Data
Linear Algebra Learning From Data 1.1 Multiplication Ax Using Columns of A 有关于矩阵乘法的理解深入 矩阵乘法理解为左侧有是一 ...
- Linear Algebra lecture6 note
Vector spaces and subspaces Column space of A solving Ax=b Null space of A Vector space requiremen ...
- Linear Algebra Lecture5 note
Section 2.7 PA=LU and Section 3.1 Vector Spaces and Subspaces Transpose(转置) example: 特殊情况,对称 ...
- Linear Algebra lecture1 note
Professor: Gilbert Strang Text: Introduction to Linear Algebra http://web.mit.edu/18.06 Lecture 1 ...
- 算法库:基础线性代数子程序库(Basic Linear Algebra Subprograms,BLAS)介绍
调试DeepFlow光流算法,由于作者给出的算法是基于Linux系统的,所以要在Windows上运行,不得不做大量的修改工作.移植到Windows平台,除了一些头文件找不到外,还有一些函数也找不到.这 ...
- 《Linear Algebra and Its Applications》-chaper4-向量空间-子空间、零空间、列空间
在线性代数中一个非常重要的概念就是向量空间R^n,这一章节将主要讨论向量空间的一系列性质. 一个向量空间是一些向量元素构成的非空集合V,需要满足如下公理: 向量空间V的子空间H需要满足如下三个条件: ...
- 《Linear Algebra and Its Applications》-chaper6-正交性和最小二乘法-基本概念与定理
这一章节我们主要讨论定义在R^n空间上的向量之间的关系,而这个关系概括来讲其实就是正交,然后引入正交投影.最佳逼近定理等,这些概念将为我们在求无解的线性方程组Ax=b的最优近似解打下基石. 正交性: ...
随机推荐
- Spring用到了那些注解?
一:@Autowired(按类型注入)1.1通过 @Autowired的使用来消除 set ,get方法.@Autowiredprivate Dao dao;这样就可以删除set ,get方法和spr ...
- OSCP Learning Notes - WebApp Exploitation(5)
Remote File Inclusion[RFI] Prepare: Download the DVWA from the following website and deploy it on yo ...
- 为啥Underlay才是容器网络的最佳落地选择
导语: 几年前,当博云启动自研容器网络研发的时候,除了技术选型的考虑,我们对于先做 Underlay 还是 Overlay 网络也有过深度的讨论.当时的开源社区以及主流容器厂商,多数还是以 Overl ...
- 题解 SP2713 【GSS4 - Can you answer these queries IV】
用计算器算一算,就可以发现\(10^{18}\)的数,被开方\(6\)次后就变为了\(1\). 所以我们可以直接暴力的进行区间修改,若这个数已经到达\(1\),则以后就不再修改(因为\(1\)开方后还 ...
- 微信小程序 springboot nginx 做图片存储 上传 浏览
微信小程序前端-springboot后端-nginx图片存储 前言 本人小白一名,这是第一次学习微信小程序,特此做个记录. 首先准备nginx做图片存储 选择一个地址存放图片 #我的地址 [root@ ...
- 微型计算机系统实验总结(学习性实验:IO地址译码,可编程并行接口8255,交通灯控制实验 + 自主设计实验:汽车信号灯控制系统,电风扇控制器,洗衣机控制系统,霓虹灯,电梯控制系统)
实验配套软件: https://download.csdn.net/download/qq_39932172/11221584 实验指导用书: 教师版: https://download.csdn.n ...
- PPT如何转换为Word文档?
首先,打开你要转换的PPT,按F12键,此时会跳出另存为窗口,如图: 然后点击保存类型,选择RTF文件,保存到指定路径即可. 找到保存好的RTF文件,用word打开即可.
- form表单两种提交方式的不同
我们在使用<Form>表单的时候,最常用的提交方式就是Get和Post.我们都知道这两种方式最大的差别就是安全性,除此之外,它们还有哪些其他的区别,你知道吗? 在<Form& ...
- python Web项目上线之服务器环境配置
1.下载安装Xftp 安装成功后,登录服务器用户密码,登录成功后 使用Xftp 将下载好的python解释器linux压缩包放置在服务器根目录下(这里用的是python3.7) 2. 解压压缩包,安装 ...
- cookie 和session的简单比较
1.cookie数据存放在客户的浏览器上,session数据放在服务器上. 2.cookie不是很安全,别人可以分析存放在本地的COOKIE并进行COOKIE欺骗 考虑到安全应当使用session ...
