Mutual information and Normalized Mutual information 互信息和标准化互信息

实验室最近用到nmi( Normalized Mutual information )评价聚类效果,在网上找了一下这个算法的实现,发现满意的不多.

浙江大学蔡登教授有一个，http://www.zjucadcg.cn/dengcai/Data/code/MutualInfo.m ，他在数据挖掘届地位很高,他实现这个算法的那篇论文引用率高达三位数。但这个实现，恕个人能力有限，我实在是没有看懂:变量命名极为个性，看的如坠云雾；代码倒数第二行作者自己添加注释why complex，我就更不懂了；最要命的是使用他的函数MutualInfo(L1,L2)得到的结果不等于MutualInfo(L2,L1)，没有对称性！

还有个python的版本http://blog.sun.tc/2010/10/mutual-informationmi-and-normalized-mutual-informationnmi-for-numpy.html，这个感觉很靠谱，作者对nmi的理解和我是一样的。

我的理解来自wiki和stanford，其实很简单，先说一下问题：例如stanford中介绍的一个例子：

比如标准结果是图中的叉叉点点圈圈，我的聚类结果是图中标注的三个圈。

或者我的结果: A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];

标准的结果   : B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];

问题：衡量我的结果和标准结果有多大的区别，若我的结果和他的差不多，结果应该为1，若我做出来的结果很差，结果应趋近于0。

MI可以按照下面的公式计算。X=unique(A)=[1 2 3]，Y=unique(B)=[1 2 3];

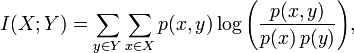
分子p(x,y)为x和y的联合分布概率，

p(1,1)=5/17, p(1,2)=1/17, p(1,3)=0;

p(2,1)=1/17, p(2,2)=4/17, p(2,3)=1/17;

p(3,1)=2/17, p(3,2)=0, p(3,3)=3/17;

分母p(x)为x的概率函数，p(y)为y的概率函数，x和y分别来自于A和B中的分布，所以即使x=y时，p(x)和p(y)也可能是不一样的。

对p(x)： p(1)=6/17 p(2)=6/17 p(3)=5/17

对p(y)： p(1)=8/17 p(2)=5/17 P(3)=4/17

这样就可以算出MI值了。

标准化互聚类信息也很简单，有几个不同的版本，大体思想都是相同的，都是用熵做分母将MI值调整到0与1之间。一个比较多见的实现是下面所示：

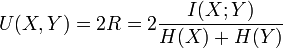
H(X)和H(Y)分别为X和Y的熵，下面的公式中log的底b=2。

例如H(X) =  -p(1)*log2(p(1)) - -p(2)*log2(p(2)) -p(3)*log2(p(3))。

matlab实现代码如下

function MIhat = nmi( A, B ) 
%NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% Author: http://www.cnblogs.com/ziqiao/   [2011/12/13] 
if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
end
total = length(A);
A_ids = unique(A);
B_ids = unique(B);

% Mutual information
MI = 0;
for idA = A_ids
    for idB = B_ids
         idAOccur = find( A == idA );
         idBOccur = find( B == idB );
         idABOccur = intersect(idAOccur,idBOccur); 
         
         px = length(idAOccur)/total;
         py = length(idBOccur)/total;
         pxy = length(idABOccur)/total;
         
         MI = MI + pxy*log2(pxy/(px*py)+eps); % eps : the smallest positive number

    end
end

% Normalized Mutual information
Hx = 0; % Entropies
for idA = A_ids
    idAOccurCount = length( find( A == idA ) );
    Hx = Hx - (idAOccurCount/total) * log2(idAOccurCount/total + eps);
end
Hy = 0; % Entropies
for idB = B_ids
    idBOccurCount = length( find( B == idB ) );
    Hy = Hy - (idBOccurCount/total) * log2(idBOccurCount/total + eps);
end

MIhat = 2 * MI / (Hx+Hy);
end

% Example :  
% (http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html)
% A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
% B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
% nmi(A,B)
% ans = 0.3646  

为了节省运行时间，将for循环用矩阵运算代替，1百万的数据量运行 1.795723second，上面的方法运行3.491053 second；

但是这种方法太占内存空间， 五百万时，利用matlab2011版本的内存设置就显示Out of memory了。

function MIhat = nmi( A, B )
%NMI Normalized mutual information
% http://en.wikipedia.org/wiki/Mutual_information
% http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
% Author: http://www.cnblogs.com/ziqiao/   [2011/12/15] 
if length( A ) ~= length( B)
    error('length( A ) must == length( B)');
end
total = length(A);
A_ids = unique(A);
A_class = length(A_ids);
B_ids = unique(B);
B_class = length(B_ids);
% Mutual information
idAOccur = double (repmat( A, A_class, 1) == repmat( A_ids', 1, total ));
idBOccur = double (repmat( B, B_class, 1) == repmat( B_ids', 1, total ));
idABOccur = idAOccur * idBOccur';
Px = sum(idAOccur') / total;
Py = sum(idBOccur') / total;
Pxy = idABOccur / total;
MImatrix = Pxy .* log2(Pxy ./(Px' * Py)+eps);
MI = sum(MImatrix(:))
% Entropies
Hx = -sum(Px .* log2(Px + eps),2);
Hy = -sum(Py .* log2(Py + eps),2);
%Normalized Mutual information
MIhat = 2 * MI / (Hx+Hy);
% MIhat = MI / sqrt(Hx*Hy); another version of NMI
end

% Example :  
% (http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html)
% A = [1 1 1 1 1 1   2 2 2 2 2 2    3 3 3 3 3];
% B = [1 2 1 1 1 1   1 2 2 2 2 3    1 1 3 3 3];
% nmi(A,B) 
% ans =  0.3646

参考： stanford的讲解：http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html

wiki百科的讲解：http://en.wikipedia.org/wiki/Mutual_information

某作者的python的实现：http://blog.sun.tc/2010/10/mutual-informationmi-and-normalized-mutual-informationnmi-for-numpy.html

蔡登的matlab实现：http://www.zjucadcg.cn/dengcai/Data/code/MutualInfo.m