《机器学习实战》学习笔记第十三章 —— 利用PCA来简化数据

相关博文：

吴恩达机器学习笔记（八） —— 降维与主成分分析法(PCA)

主成分分析（PCA）的推导与解释

主要内容：

一.向量內积的几何意义

二.基的变换

三.协方差矩阵

四.PCA求解

一.向量內积的几何意义

1.假设A、B为二维平面xoy内两个向量，A为(x1, y1)，B为(x2, y2)，那么A、B的內积为：AB = |A||B|cosΘ = x1*x2 + y1*y2，结果为一个标量。

2.那么A、B內积的几何意义又是什么呢？单从“|A||B|cosΘ”或者“x1*x2 + y1*y2”这两式子或许还不能发现其中的意义，那么可以在坐标轴上画出这两个向量：

可以看出，|A|cosΘ实际上就是向量A在向量B方向上的投影。假如B为单位向量，即|B| = 1，那么A、B的內积就是A向量在B向量上的投影。

综上：假设B向量为单位向量，那么A、B的內积为：A向量在B向量上的投影，且AB = |A||B|cosΘ = x1*x2 + y1*y2。

二.基的变换

1.基变换，就是用新的正交轴去代替旧的正交轴（原定固定），旧的正交轴就是我们日常所使用的XOY坐标轴，其基向量为 i(1,0) 和 j(0,1)。

注意：基向量必须为单位向量且两两正交（我目前的认知）。

2.例如，有一个向量a在旧坐标轴表示为 (3, 2)，我们重新构建一个坐标轴，其基向量分别为 (1/√2，1/√2)和(-1/√2，1/√2)。那么向量a在新坐标轴上表示为 (5/√2，-1/√2)。

3.更一般地：

（注意，新坐标轴的基向量的表示仍然是基于旧坐标轴而言的。）

4.问：为什么新坐标轴的基向量的模要为1且要两两正交？

答：两两正交的单位基向量组成了“标准正交向量组”，将他们按列排成一个矩阵，此矩阵就是“正交矩阵”，同时也可以称为是变换矩阵，即可将向量从旧的坐标轴表示转化为新的坐标轴表示，这个过程就成为“正交变换”，而正交变换不改变向量的內积，从而不改变向量的模、夹角和距离，即不改变形状，而只不过是换了另一种表示。

5.课本上正交矩阵的定义：加入矩阵A满足 A' A = I，则称A为正交矩阵。那么为什么正交矩阵与自身的转置做乘法，会得到一个单位矩阵呢？

答：首先，A'实质上是n个行向量，每一个行向量就是对应的新坐标系的基向量，那么：

1）当这个行向量（在A'上）与自己对应的列向量（在A上）做內积时，结果必定为1（根据內积的几何意义：內积为投影，自己对自己的投影当然就为1了）。

2）当这个行向量（在A'上）与自己别的列向量（在A上）做內积时，结果必定为0，因为这n个向量两两正交，所以內积为0。

综上：只有当“自己与自己”做內积时，结果为1,其他情况为0，所以正交矩阵A满足：A' A = I。

三.协方差矩阵

1.假如我们想重新构建一个能高效表达数据信息的坐标系，所谓“高效”就是信息尽量集中在少数几个或一小部分坐标轴中，而其他坐标轴几乎不含有信息（之后在PCA中就可以去掉这些坐标轴，即减少特征，从而实现降维）。那么怎么衡量坐标轴上信息的多少呢？可以用方差。一般地，在某个坐标轴上，假设数据的方差越大，那么我们可以认为数据在这个坐标轴上所含有的信息量越大。

2.假如，我们想从n维降到k维，那么是不是意味着只需要挑选出前k个方差最大的坐标轴（或者是特征）作为新的坐标系就可以呢？

答：非也！方差最大的轴作为第一维是可以肯定的，但是方差第二大的轴选作第二维却未必。因为方差第二大的轴可能与方差第一大的轴有很强的关联性，转成机器学习的语言就是：两个特征有很强的关联性，这就代表了两个轴之间有很大一部分的信息是重叠了的，即使两者都含有很多信息。对此，能够表示两个不同特征之间关联性的“好汉”是协方差矩阵。

3.协方差矩阵上，对角线表示的是每个特征的方差；而对角线外的表示两个不同特征之间的相关性，大于0时表示两者正相关，小于0则负相关，且绝对值越大，则相关性越强。特别地，当等于0时，表示两特征不相关，即相互独立。（推荐博文以更好地理解协方差矩阵：终于明白协方差的意义了）

4.如何求协方差矩阵？

1）首先对特征进行归一化。为何要归一化？因为特征之间的取值范围的差异可能很大，为了排除这个因素的干扰，需要将它们全都归到一个梯度上去，从而使得方差或者协方差才有可比性。（但我看到《机器学习实战》上的代码没有归一化，不知为何？）

2）假设经过归一化的输入数据为X，协方差矩阵为Σ，那么：

5.得到协方差矩阵，即知道了每两两特征之间的相关性，那这对于选取k个信息最大的特征又有和帮助呢？请看下回（节）分解。

四.PCA求解

1.假设归一化后的输入数据X的协方差矩阵为Cx，为了能够更加高效地表示数据，我们重新构造出一个坐标系（基向量仍然为n个，后面再挑选出最好的k个），假设这个坐标系的基向量所构成的矩阵为P（n个列向量），可知P为正交矩阵（在手写的那一大段文字有解释）。接下来将X从原来的坐标系转换到新的坐标系，那么新的坐标表示为：Y = X*P。

2.假设Y的协方差矩阵为Cy，那么我们的目标就是：求出这个正交变换P（也就是求出这个新的坐标系），使得协方差矩阵Cy上除了对角线之外的其他元素都为0，从而使得每两两特征之间都互不相关，于是就可以单凭数据在特征上的方差选出含信息量最大的那k个特征。

3.有了目标之后，就尝试从公式下手：

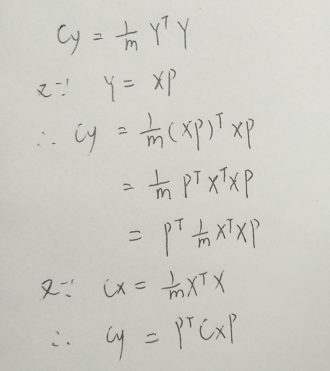
4.从形式上看，不就是要我们对Cx对角化吗？更准确地：因为Cx为是实对称矩阵，所以必定有正交矩阵P满足条件（定理来的）。

至于对角化，我们只需要求出Cx的特征向量，就可以组合成正交矩阵P了。而这些特征向量，就是我们重新构建出来的那n个在新坐标系上的坐标轴，即新特征。

5.那么又怎么从中挑选出含信息量最大的k个坐标轴呢？

答：这就要回看协方差矩阵Cy，它是一个对角矩阵，对角线上的元素就是Cy的特征值，更重要的是：他们就是在新坐标系上每个坐标轴（应该叫做特征比较合适）的方差，那么只需对这些方差排个序，选出前k个特征值对应的特征向量，以此组成新的维度更少的坐标系、组成新的更少的特征，从而实现降维，这就是PCA。