1135 Is It A Red-Black Tree（30 分）

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

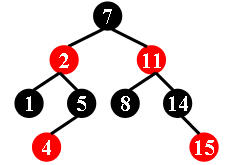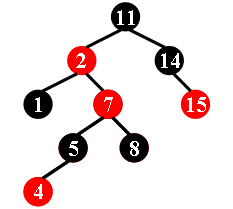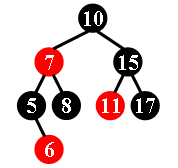Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line "Yes" if the given tree is a red-black tree, or "No" if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

Yes
No
No


要求题目中写的很清楚，红黑树是二叉搜索树，所以给出前序遍历，那么中序遍历也可以知道（从小到大排序就是中序遍历)，但负号不是代表大小，所以排序前，要取绝对值，然后建树，进行判断，按照题目要求，根结点必须是黑的（正的），
红色的儿子必须都是黑色，从某个点到所有的子孙叶子结点的路径包含黑色点个数相同。
代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;

struct tree {
    int data;
    tree *left,*right;
};
int pre[],in[];
int k,n,flag;
tree *build(int pre_l,int pre_r,int in_l,int in_r) {
    tree *t = new tree();
    t -> left = t -> right = NULL;
    for(int i = in_l;i <= in_r;i ++) {
        if(in[i] == abs(pre[pre_l])) {
            if(i != in_l)t -> left = build(pre_l + ,pre_l + i - in_l,in_l,i - );
            if(i != in_r)t -> right = build(pre_l + i - in_l + ,pre_r,i + ,in_r);
            break;
        }
    }
    t -> data = pre[pre_l];
    return t;
}
int check(tree *t) {
    if(t == NULL)return ;
    if(t -> data <  && (t -> left && t -> left -> data <  || t -> right && t -> right -> data < )) {
        flag = ;
        return ;
    }
    int d = check(t -> left),e = check(t -> right);
    if(d != e)flag = ;
    return d + (t -> data > );///如果颜色为黑色，返回值加1
}
void drop(tree *t) {
    if(t == NULL)return;
    drop(t -> left);
    drop(t -> right);
    delete t;
}
int main() {
    scanf("%d",&k);
    while(k --) {
        scanf("%d",&n);
        for(int i = ;i < n;i ++) {
            scanf("%d",&pre[i]);
            in[i] = abs(pre[i]);///取绝对值
        }
        flag = ;
        sort(in,in + n);
        tree *head = build(,n - ,,n - );///建树
        if(head -> data < )flag = ;///根结点不是黑色
        else check(head);///检查是否满足
        drop(head);///释放空间
        puts(flag ? "Yes" : "No");
    }
}