「P4994」「洛谷11月月赛」终于结束的起点（枚举

题目背景

终于结束的起点
终于写下句点
终于我们告别
终于我们又回到原点
……

一个个 OIer 的竞赛生涯总是从一场 NOIp 开始，大多也在一场 NOIp 中结束，好似一次次轮回在不断上演。
如果这次 NOIp 是你的起点，那么祝你的 OI 生涯如同夏花般绚烂。
如果这次 NOIp 是你的终点，那么祝你的 OI 回忆宛若繁星般璀璨。
也许这是你最后一次在洛谷上打比赛，也许不是。
不过，无论如何，祝你在一周后的比赛里，好运。

当然，这道题也和轮回有关系。

题目描述

广为人知的斐波拉契数列 \mathrm{fib}(n)fib(n) 是这么计算的

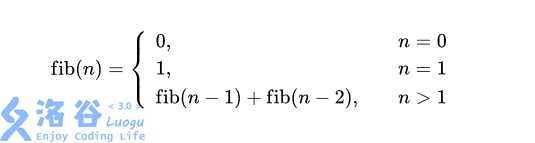
也就是 0, 1, 1, 2, 3, 5, 8, 13 \cdots0,1,1,2,3,5,8,13⋯，每一项都是前两项之和。

小 F 发现，如果把斐波拉契数列的每一项对任意大于 11 的正整数 MM 取模的时候，数列都会产生循环。

当然，小 F 很快就明白了，因为 (\mathrm{fib}(n - 1) \bmod Mfib(n−1)modM) 和 (\mathrm{fib}(n - 2) \bmod M)fib(n−2)modM) 最多只有 M ^ 2M2 种取值，所以在 M ^ 2M2 次计算后一定出现过循环。

甚至更一般地，我们可以证明，无论取什么模数 MM，最终模 MM 下的斐波拉契数列都会是 0, 1, \cdots, 0, 1, \cdots0,1,⋯,0,1,⋯。

现在，给你一个模数 MM，请你求出最小的 n > 0n>0，使得 \mathrm{fib}(n) \bmod M = 0, \mathrm{fib}(n + 1) \bmod M = 1fib(n)modM=0,fib(n+1)modM=1。

输入输出格式

输入格式：

输入一行一个正整数 MM。

输出格式：

输出一行一个正整数 nn。

输入输出样例

输入样例#1：复制

输出样例#1：复制

输入样例#2：复制

输出样例#2：复制

说明

样例 1 解释

斐波拉契数列为 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \cdots0,1,1,2,3,5,8,13,21,34,⋯，在对 22 取模后结果为 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, \cdots0,1,1,0,1,1,0,1,1,0,⋯。

我们可以发现，当 n = 3n=3 时，f(n) \bmod 2= 0, f(n + 1) \bmod 2 = 1f(n)mod2=0,f(n+1)mod2=1，也就是我们要求的 nn 的最小值。

数据范围

对于 30\%30% 的数据，M \leq 18M≤18；

对于 70\%70% 的数据，M \leq 2018M≤2018；

对于 100\%100% 的数据，2 \leq M \leq 706150=2≤M≤706150=0xAC666。

提示

如果你还不知道什么是取模 (\bmod)(mod)，那我也很乐意告诉你，模运算是求整数除法得到的余数，也就是竖式除法最终「除不尽」的部分，也即a \bmod M =k \iff a = bM + k\ (M > 0, 0 \leq k < M)amodM=k⟺a=bM+k (M>0,0≤k<M)其中 a, b, ka,b,k 都是非负整数。

如果你使用 C / C++，你可以使用 % 来进行模运算。

如果你使用 Pascal，你可以使用 mod 来进行模运算。

题解

如果这次 NOIp 是你的终点，那么祝你的 OI 回忆宛若繁星般璀璨。

哈哈哈哈为什么要一上来就放催泪弹啊一点都不感动嘤嘤嘤嘤

一开始淡定的打表找规律，发现跟因子有些关系，大概就是对很多数而言是质因子的f乘起来再乘反复出现的质因子之类......

然后不想肝了挂了个机跑1~706150的答案，记了个最大值，好像最大值只是个211多少的七位数......

那还规律个鬼啊，暴力啊！

 /*

 qwerta

 P4994 终于结束的起点 Accepted

 100

 代码 C++，0.25KB

 比赛 【LGR-055】洛谷11月月赛

 提交时间 2018-11-04 09:08:05

 耗时/内存 70ms, 808KB

 */

 #include<iostream>

 #include<cstdio>

 #include<cmath>

 using namespace std;

 int main()

 {

     int m;

     scanf("%d",&m);

     int f0=,f1=;

     for(long long n=;;++n)

     {

         int x=(f0+f1)%m;

         if(f1==&&x==)

         {

             cout<<n;

             break;

         }

         f0=f1;

         f1=x;

     }

     return ;

 }