Applied Nonparametric Statistics-lec3

Ref:

https://onlinecourses.science.psu.edu/stat464/print/book/export/html/4

---

使用非参数方法的优势：

1. 对总体分布做的假设少，所以总体分布未知也可以；

2. 容易做；

3. 一般对离群值更具鲁棒性robust；

4. 适用于数据中包含ranks, ordinal or categorical的。

In a skewed distribution, the population median, η, is a better typical value than the population mean μ.

Sign-test / Binomial-test:

下面是一个实例：

这个实例，我们先用t-test。做的假设是，数据为正态分布，所以使用t-statistics，检验的是均值μ。

然后，考虑到数据是有偏的，我们使用中值median，然后用sign-test。

Solution：这样计算的概率是p值。如此，我们不能拒绝原假设。

当数据量大时：

If np ≥ 10 and n(1 - p)  ≥ 10, we can use the Normal distribution to approximate the Binomial.

然后可以使用z-score。注意，此时方差和均值的取值。后面假设检验的部分与lec2中内容一致。

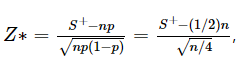
求置信区间：

Type I error是错误拒绝原假设；Type II error是错误接受原假设。

The significance level of the test is α = P(Type I error)

Power = 1 - P(Type II error)

如果两个test的α相等，那么power大的那个更好。

在实际操作中，使用R语言的包BSDA

SIGN.test(x, md = 0, alternative = "two.sided", conf.level = 0.95)
# x - is the object where you store your data
# md - the hypothesized median (default is 0)
# alternative - either "two.sided", "greater", or "less than"
# conf.level  - the desired confidence level.