GCOV&LCOV&GCOVR入门

索引

1. 一、概述
2. 二、关于gcov的安装
3. 三、代码覆盖率测试（以GCOV为例）
   • 1、编译源代码
   • 2、运行可执行程序
   • 3、通过gcov指令生成代码覆盖率报告
4. 四、生成更全面、直观的代码覆盖率报告
   • 1、LCOV
   • 2、GCOVR
5. 五、参考

一、概述

代码覆盖率（Code coverage）是衡量软件测试质量的一个重要指标。

它描述了当一个特定的测试套件（test suite）运行时，程序源代码被执行的程度。例如，一些更具体的覆盖率指标有：

1. Statement Coverage：描述源代码中有哪些代码行被执行，各自被执行了多少次
2. Branch coverage：一般用于描述if语句/或其它条件语句的各分支的执行情况
3. Function coverage：顾名思义，描述源代码中有哪些函数被执行了
4. ······

代码覆盖率测试工具可以帮助我们发现代码中未被测试的部分，

而gcov则是一款和GCC配套发布的[经典]代码覆盖率分析工具（仅仅是对覆盖率信息文件进行分析）。

同为代码覆盖率分析工具，GCOV&LCOV&GCOVR之间的差异：

• GCOV：与GCC配套，不需要安装，生成纯文本文件
• LCOV：需要安装，跨平台麻烦，生成HTML页面
• GCOVR：需要安装，跨平台容易，且指令比LCOV少，生成HTML页面

PS. 不仅仅是C或者C++，GCC所支持的语言它们应该都是支持的，例如说Fortran

二、关于gcov的安装

gcov是随gcc一起发布的，并不需要独立安装，设法装上gcc就OK了。对于WINDOWS系统，通过MinGW安装gcc相关的组件即可使用gcov。而对于Linux系统而言，通常会默认安装gcc，因此一般不需要自己安装。

三、代码覆盖率测试（以GCOV为例）

首先，我们需要通过gcc的编译选项获取覆盖率信息文件（例如每行代码被执行了多少次啊），

这里的“生成覆盖率信息”的步骤对任何一个覆盖率分析工具都是完全一样的，

然后，用gcov收集、分析覆盖率信息文件并生成代码覆盖率报告。

用于演示的C程序源代码（包含一个计算阶乘的函数）：

#include <stdio.h>

int factorial(int n);

int main()
{
    int result0 = factorial();
    int result1 = factorial();
    int result2 = factorial();

    if (result0 != ) printf("test0 failed, actual=%d.\n", result0);
    if (result1 != ) printf("test1 failed, actual=%d.\n", result1);
    if (result2 != ) printf("test2 failed, actual=%d.\n", result2);

    return ;
}

int factorial(int n)
{
    if (n < ) {
        printf("Factorial is defined only for non-negative integer numbers.");
        return -;
    }

    if (n > ) {
        return n * factorial(n - );
    } else {
        return ;
    }
}

factorial.c

1、编译源代码

要生成覆盖率信息文件，必须添加以下编译选项：

gcc -fprofile-arcs -ftest-coverage factorial.c

将factorial.c编译之后，我们将得到一个被“改造”过的可执行程序a.exe，该程序中包含了一些额外的指令，用于记录程序中每一行被执行的次数。以及一个后缀为.gcno的factorial.gcno文件，它是即将被gcov引用的关键数据文件。

编译选项说明：

• -ftest-coverage选项：添加记录单行代码执行次数的指令
• -fprofile-arc选项：添加程序每个分支的检测代码（if或者其它条件语句）

2、运行可执行程序

./a.exe

运行可执行程序之后，我们会得到一个factorial.gcda的文件，它和factorial.gcno一样是即将被gcov引用的数据文件（代码覆盖率信息文件）。

3、通过gcov命令生成代码覆盖率报告

gcov factorial.c
File 'factorial.c'
Lines executed:86.67% of
Creating 'factorial.c.gcov'

执行指令后，gcov会引用之前的数据文件生成一个代码覆盖率报告factorial.c.gcov：

$ cat factorial.c.gcov
        -:    :Source:factorial.c
        -:    :Graph:factorial.gcno
        -:    :Data:factorial.gcda
        -:    :Runs:
        -:    :Programs:
        -:    :#include <stdio.h>
        -:    :
        -:    :int factorial(int n);
        -:    :
        :    :int main()
        -:    :{
        :    :        int result0 = factorial();
        :    :        int result1 = factorial();
        :    :    int result2 = factorial();
        -:   :
        :   :        if (result0 != ) printf("test0 failed, actual=%d.\n", result0);
        :   :        if (result1 != ) printf("test1 failed, actual=%d.\n", result1);
        :   :        if (result2 != ) printf("test2 failed, actual=%d.\n", result2);
        -:   :
        :   :    return ;
        -:   :}
        -:   :
       :   :int factorial(int n)
        -:   :{
       :   :        if (n < ) {
    #####:   21:                printf("Factorial is defined only for non-negative integer numbers.");
    #####:   22:                return -1;
        -:   :        }
        -:   :
       :   :    if (n > ) {
        :   :                return n * factorial(n - );
        -:   :        } else {
        :   :                return ;
        -:   :        }
        -:   :}

“#####”所标记的是未被执行的语句。

四、生成更全面、直观的代码覆盖率报告

直接用gcov生成的代码覆盖率报告并不是很直观，因此一般应该都是用以下两款。

1、LCOV

Lcov是gcov的图形化前端，它和GCOV做的工作是差不多的，只不过最后输出的是HTML页面形式的代码覆盖率报告。

Ubuntu系统下安装LCOV：

sudo apt-get install lcov

依然用之前的factorial.c演示。首先，按之前的步骤生成相关数据文件，例如xxx.gcda、xxx.gcno（PS. 不需要用gcov生成xxx.c.gcov文件）。然后，用LCOV收集相关数据并生成一个.info文件（方便起见直接在当前目录执行该命令）：

lcov --capture --directory . --output-file coverage.info

最后，通过genhtml将coverage.info转化为HTML文件（genhtml是lcov自带的工具）：

genhtml coverage.info --output-directory out

生成的OUT目录里包含了HTML版的代码覆盖率报告。

在WINDOWS上安装LCOV比较繁琐，有人专门写了Windows上可运行的LCOV脚本[LCOV for Windows]，但是我下载下来后没弄懂怎么用。

2、GCOVR

相比于LCOV，gcovr可能更方便一点。LCOV有的功能gcovr都有，并且gcovr也是开源的：https://github.com/gcovr/gcovr。它是用Python写的，这意味着只要有Python环境都可以使用gcovr，无论是WINDOWS还是LINUX。直接通过pip（Python的包管理工具）安装GCOVR：

pip install gcovr

还是和之前一样的步骤生成相关的代码覆盖率信息文件，然后直接用gcovr生成HTML代码覆盖率报告就行了：

gcovr -r . --html --html-details -o coverage.html

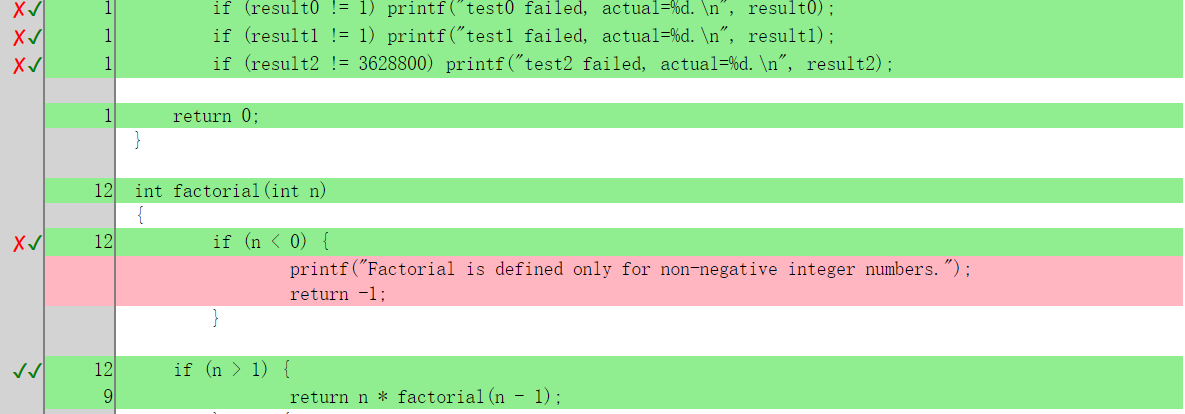
五、参考

• 代码覆盖工具(gcov、lcov)的使用 - 步孤天 - 博客园
• [整理] gcov lcov 覆盖c/c++项目入门 - turtle_fly - 博客园
• Using the GNU Compiler Collection (GCC): Gcov
• Gcov - Wikipedia