AI之旅（3）：升维与最小二乘法

前置知识

  矩阵的逆

知识地图

  首先我们将了解一种叫升维的方法，用已有特征构造更多的特征。接着通过对空间与投影建立一定的概念后，推导出最小二乘法。

当特征数量不足时

  在上一篇《初识线性回归》中，我们假设要处理的问题有足够的样本数量和足够的特征数量。记得样本数量是用m表示，特征数量是用n表示。假如只有1个特征该如何构建模型呢？

  假设现在有一个数据集，数据集中只包含一个地区房屋的面积信息和销售情况。即只有面积这一个特征，如何只用一个特征来预测房屋的销售情况呢？

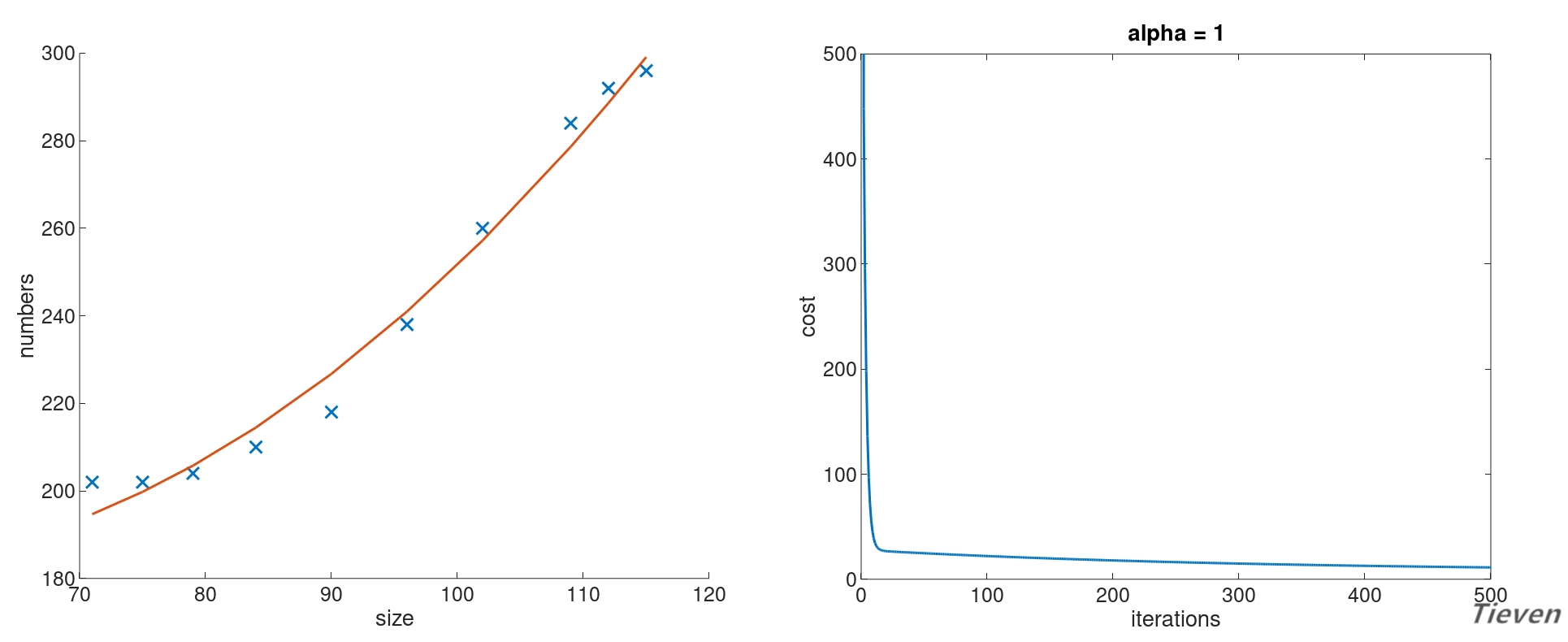
  可视化能帮助我们更好地了解数据间隐藏的规律，先来看一看数据之间的分布情况。

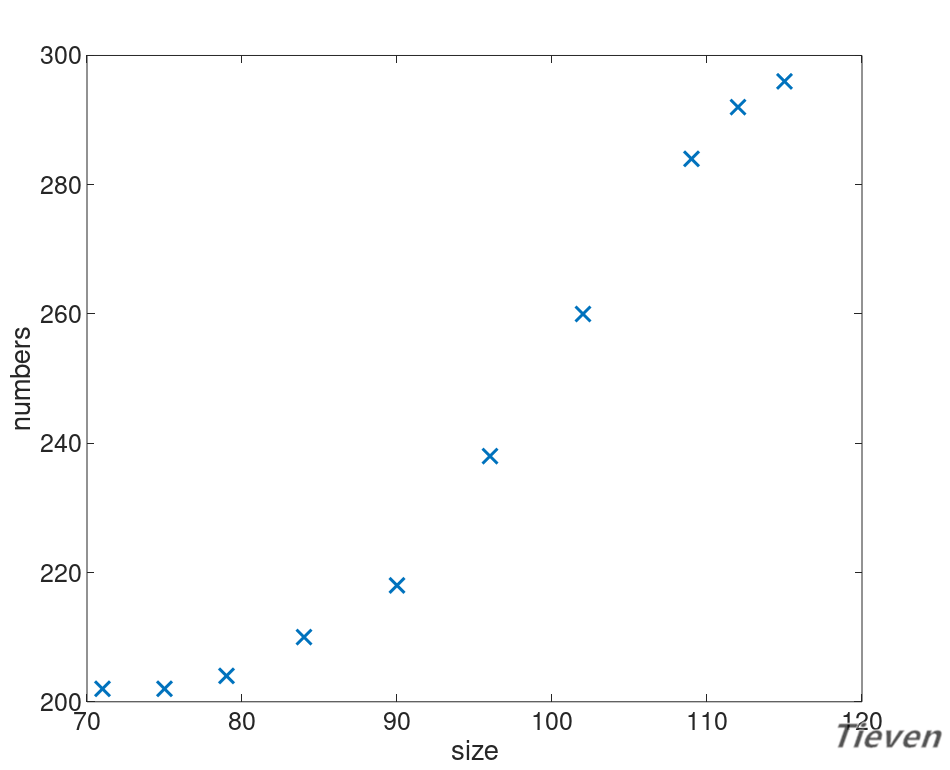
  用什么模型可以比较好地拟合数据呢？首先尝试用一条直线来拟合数据，构建一个线性模型：

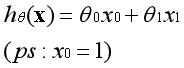
关于常数项的说明

  还记得在上一篇中讲过，线性回归模型中需要在特征中手动添加一列全为1的特征。这是为什么呢？这是一个很小的但不理顺却很容易混淆的概念，值得反复强调。

  我们熟悉的直线公式是以下形式：

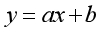
  其中a为系数，x为变量，b为常数项。常数项是用来控制直线的位置，如果没有常数项，直线会是经过原点的一条线。显然有了常数项的模型可以更好地拟合数据。

  假设函数是直线的另一种表达方式，两者是完全等价的。在直线中b是常数项，在假设函数中第一个θ参数是常数项。常数项乘以1等于本身，如下图所示。

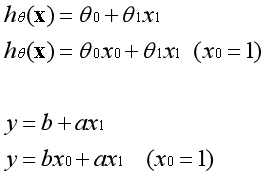
  常数项为什么要乘以1呢？因为在实际的运用中，是将参数θ视为一个向量进行运算。特征中添加全为1的一列后，可以使用向量化的方式来运算，提高了效率。

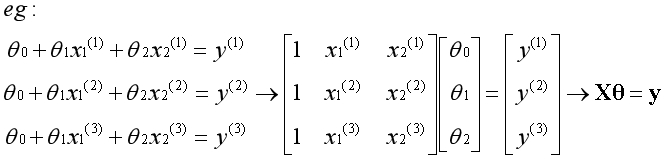
以一个特征为例

  原始数据集中特征是不包含全为1的列，将原始数据集传入函数后，在函数中额外为特征添加全为1的列，在函数中转换后的形式如下：

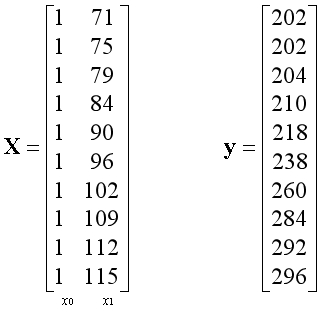
  设置学习率为0.1，迭代次数为500次。经过特征缩放，训练后得到的参数如下，其中参数的第一项可以视为常数项：

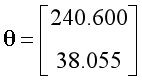
  对应的假设函数与代价函数如下：

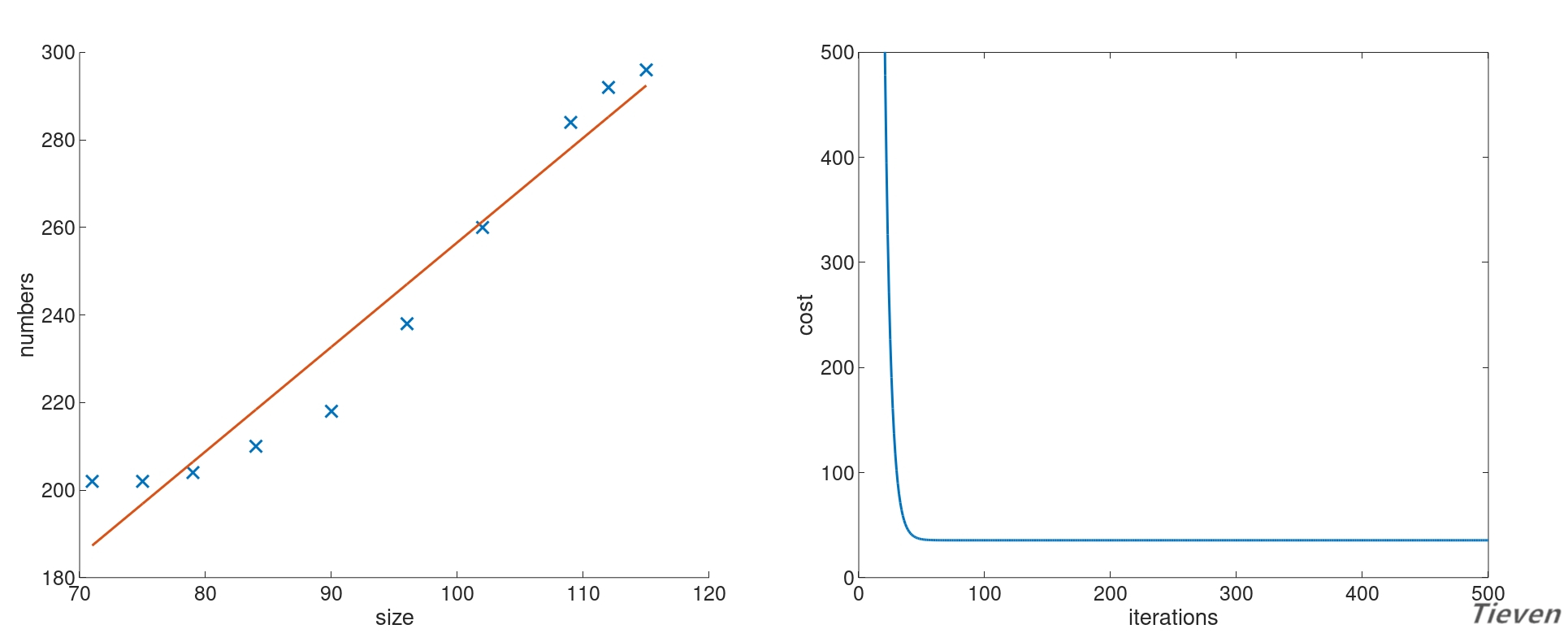
  我们发现直线似乎不能很好地揭示数据之间存在的规律，但是现在又没有更多的特征，该怎么办呢？可以用特征的平方作为新的特征添加进数据集中。

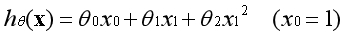
  这个模型可以视为非线性模型，同样也可以通过线性回归算法来处理，在函数中转换后的数据集的形式如下：

  增加更多的特征以后，模型会不会有更好的表现呢？

  设置学习率为0.1，迭代次数为500次。经过特征缩放，训练后得到的参数如下，其中参数的第一项可以视为常数项：

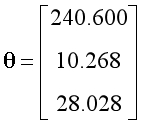
  对应的假设函数与代价函数如下：

  似乎并没有太大的改变？试试其他的学习率。

  设置学习率为1，迭代次数为500次。经过特征缩放，训练后得到的参数如下，其中参数的第一项可以视为常数项：

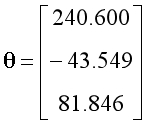
  对应的假设函数与代价函数如下：

升维的方法与局限

  可以观察到相比于直线，新的模型可以更好地拟合数据，或许也能更准确的用于预测新的数据。至此可以总结出以下两点结论：

  1，学习率需要手动调整，这实在是太不智能了，以后我们将了解不需要手动设置学习率的方法。

  2，用现有特征的2次方，3次方，4次方......来构造新的特征，可能会得到更准确的模型。

  推而广之，有一个特征的时候，可以用特征的高次方构造新的特征：

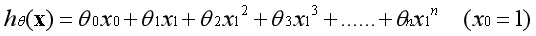
  推而广之，有多个特征的时候，可以用特征的高次方的组合构造新的特征：

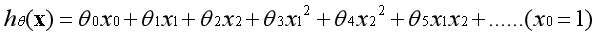
  需要注意的是，虽然用升维的方法可以构造新的特征，但是我们不想频繁地使用这种方法。如果缺少特征，首先应该想办法获取新的特征。相比于人工创造的特征，现实的特征或许会更好一些。

  比如我们有一个房子宽度的特征，和一个房子长度的特征。两者可以组合出房子面积的特征，这显然是有意义的。但是再添加面积的10次方作为新的特征，似乎失去了现实的意义，变成纯粹的数字。

一维空间与投影

  一个向量x可以构建一维空间（一条直线），另一个向量y与一维空间可以有以下几种关系：

  1，当向量y垂直一维空间时（内积为0），向量y在一维空间上的投影为0，对应的方程组无解。通过向量x无论如何也无法获得向量y。

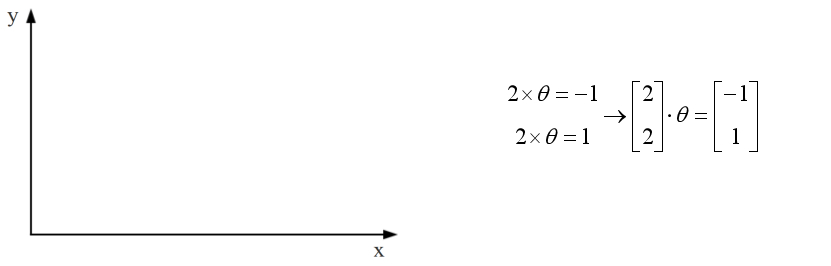
  2，当向量y平行一维空间时，向量y在一维空间上的投影为向量本身，对应的方程组有解。在向量x上乘以某一个系数可以获得向量y。

  3，当向量y与一维空间即不平行也不垂直时，向量y在一维空间上存在投影，对应的方程组无解，但存在能够得到的最优解。在向量x上乘以某一个系数，不能得到全部的向量y，但可以得到部分的向量y。

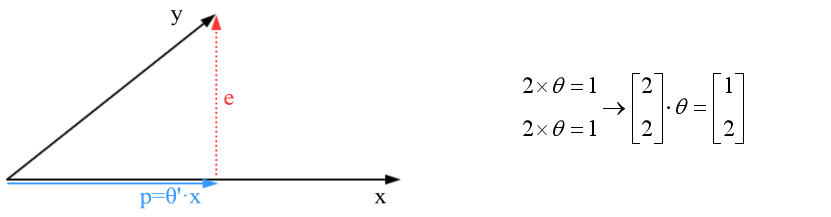
  如上图所示，向量e是误差向量，向量p是投影向量。因为向量y不在一维空间中，只能得到向量y的投影向量。类似于有人告诉你，你得不到最好的，那么现实的问题是，第二好的是什么呢？

  投影向量p是我们能得到的第二好的向量，问题转变为如何使投影向量p最大化？向量y可以分解为投影向量p与误差向量e的组合，当误差向量e最小化的时候，投影向量p最大化。

  什么情况下误差向量e最小化？当误差向量e垂直一维空间时最小化，此时有投影向量p最大化。已知两个垂直的向量内积为0，根据这一点可以建立等式。

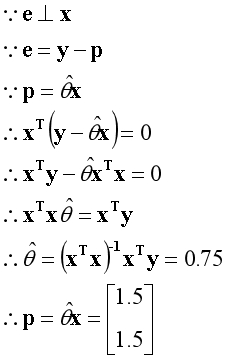
  注：此时的θ是一个标量；

二维空间与投影

  两个不在同一条直线的向量可以构建二维空间（一个平面），这两个向量称为基向量，另一个向量y与二维空间可以有以下几种关系：

  1，当向量y垂直二维空间时，向量y在二维空间上的投影为0。

  2，当向量y平行二维空间时，向量y在二维空间上的投影为向量本身。

  3，当向量y与二维空间即不平行也不垂直时，向量y在二维空间上存在投影，对应的方程组无解，但存在能够得到的最优解。在基向量上分别乘以某一个系数，不能得到全部的向量y，但可以得到部分的向量y。

  与之前类似，误差向量e同时垂直于基向量。已知两个垂直的向量内积为0，根据这一点可以建立等式。

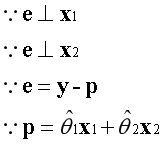
  上述是已知的信息。

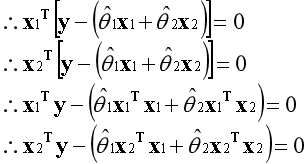
  以上等式可以写为矩阵的形式。

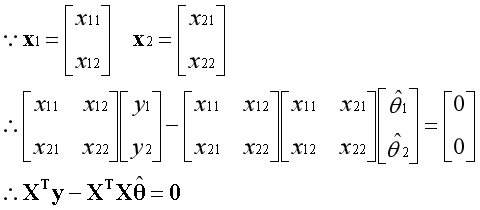
  X是基向量构成的矩阵，当矩阵可逆时，可写为如下形式。

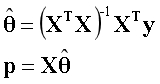
最小二乘法

  推而广之无论是2维空间，3维空间还是m维空间，道理都是一样的。如果向量不在空间内，我们只能得到向量在空间内的投影，这种获得投影的方法称为最小二乘法。

  投影是基向量的线性组合，所谓能得到的最优解，是指这个线性组合的系数。当矩阵可逆时，通过上述公式可以直接求出系数。

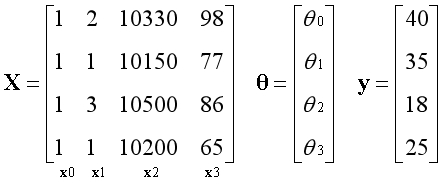
  回顾《初识线性回归》中的例子，如今我们可以从一个新的视角来看问题，矩阵X有4个线性无关的基向量，构成完整的4维空间，向量y在空间中，用最小二乘法求出最优解。

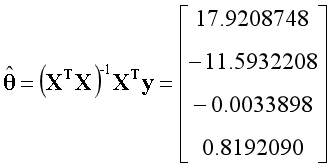
  通常数据集中样本的数量m是远远大于特征的数量n，如下图所示。

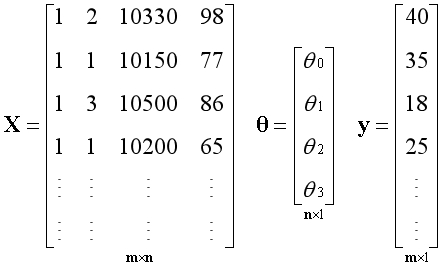
  矩阵X有n个线性无关的基向量，构成m维空间中的n维子空间，无论向量y是否在子空间内，都可以使用最小二乘法求出能得到的最优解。

  因为最小二乘法中需要对矩阵进行求逆运算，比较消耗计算资源。当我们的样本数量比较大时，比如有10万个，100万个，1000万个样本，可能就无法通过这种方法来直接计算结果。

  因此什么情况下使用最小二乘法，什么情况下使用梯度下降法，只能根据具体情况具体分析，没有一定之规。至此，我们已经掌握了求解线性回归的第二种方法。

总结

  升维是用现有特征构造更多特征的方法，特征相乘可能具有某种意义，比如已知房屋的长度和宽度可以组合出表示面积的特征。类似的，也可以将特征进行相除。

  通过从空间的角度来看待矩阵，理解投影与方程组的解之间的联系。在矩阵可逆的情况下，可以通过最小二乘法获得投影，同时也就得到了线性回归的最优解。

  虽然线性回归还有部分内容没有介绍，至少目前我们对什么是算法，算法如何工作有了感性的认识。马上，我们就能掌握第二个用于分类的算法，这将是我们接下来的旅程。

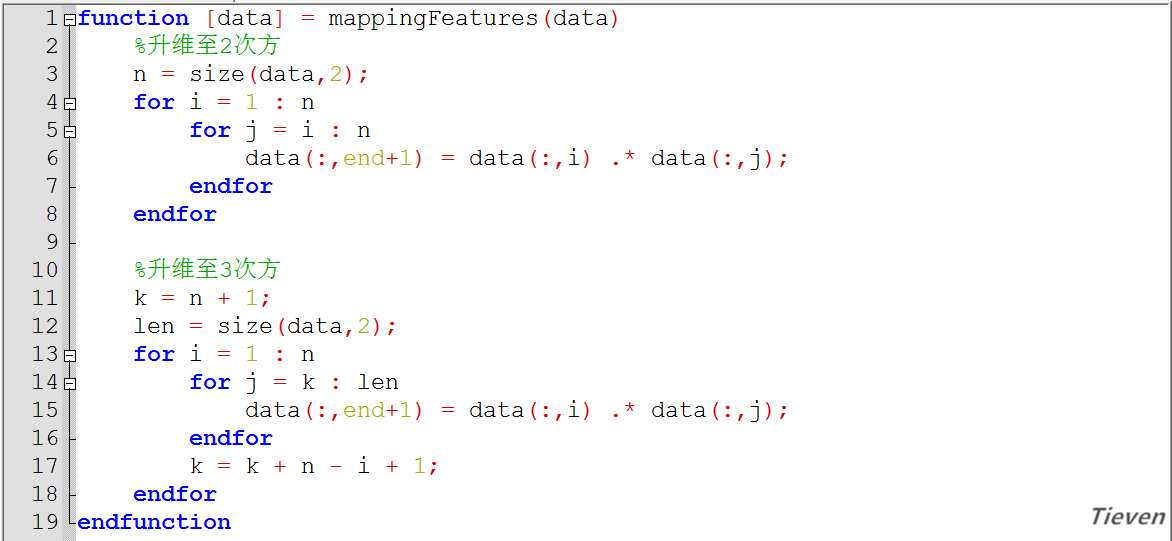
非正规代码

版权声明

  1，本文为原创文章，未经作者授权禁止引用、复制、转载、摘编。

  2，对于有上述行为者，作者将保留追究其法律责任的权利。

Tieven

2019.1.5

tieven.it@gmail.com