Java实现凸包问题

1 问题描述

给定一个平面上n个点的集合，它的凸包就是包含所有这些点的最小凸多边形，求取满足此条件的所有点。

另外，形象生动的描述：

（1）我们可以把这个问题看作如何用长度最短的栅栏把n头熟睡的老虎围起来。

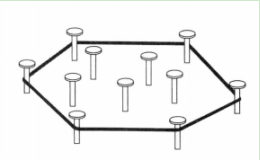
（2）也可以这样看：请把所讨论的点想象成钉在胶合板上的钉子，胶合板代表平面。撑开一根橡皮筋圈，把所有的钉子都围住，然后啪一声松开手。凸包就是以橡皮圈为边界的区域。具体示意如下图1所示：

2 解决方案

2.1 蛮力法

使用蛮力法解决此问题比较简单，具体思想：对于一个n个点集合中的两个点p1和p2，当且仅当该集合中的其它点都位于穿过这两点的直线的同一边时，它们的连线就是该集合凸包边界的一部分，简言之，p1和p2就是凸包问题中最小凸多边形的顶点。对每一对点都做一遍检验之后，满足条件的线段就构成了该凸包的边界。

此时，根据上面的公式，我们只需要把每个点代入公式ax+by-c，判断公式计算结果的符号是否全部大于等于0或者小于等于0，如果是则是凸包边界上的点，否则就不是。该算法的时间效率为0（n^3）。具体代码如下：

package com.liuzhen.chapterThree;

public class ConvexHull {
    //蛮力法解决凸包问题，返回点集合中凸多边形的点集合
    public static Point[] getConvexPoint(Point[] A){
        Point[] result = new Point[A.length];
        int len = 0;  //用于计算最终返回结果中是凸包中点的个数
        for(int i = 0;i < A.length;i++){
            for(int j = 0;j < A.length;j++){
                if(j == i)     //除去选中作为确定直线的第一个点
                    continue;

                int[] judge = new int[A.length];   //存放点到直线距离所使用判断公式的结果

                for(int k = 0;k < A.length;k++){
                    int a = A[j].getY() - A[i].getY();
                    int b = A[i].getX() - A[j].getX();
                    int c = (A[i].getX())*(A[j].getY()) - (A[i].getY())*(A[j].getX());

                    judge[k] = a*(A[k].getX()) + b*(A[k].getY()) - c;  //根据公式计算具体判断结果
                }

                if(JudgeArray(judge)){  // 如果点均在直线的一边,则相应的A[i]是凸包中的点
                    result[len++] = A[i];
                    break;
                }
            }
        }
        Point[] result1 = new Point[len];
        for(int m = 0;m < len;m++)
            result1[m] = result[m];
        return result1;
    }

    //判断数组中元素是否全部大于等于0或者小于等于0，如果是则返回true，否则返回false
    public static boolean JudgeArray(int[] Array){
        boolean judge = false;
        int len1 = 0, len2 = 0;

        for(int i = 0;i < Array.length;i++){
            if(Array[i] >= 0)
                len1++;
        }
        for(int j = 0;j < Array.length;j++){
            if(Array[j] <= 0)
                len2++;
        }

        if(len1 == Array.length || len2 == Array.length)
            judge = true;
        return judge;
    }

    public static void main(String[] args){
        Point[] A = new Point[8];
        A[0] = new Point(1,0);
        A[1] = new Point(0,1);
        A[2] = new Point(0,-1);
        A[3] = new Point(-1,0);
        A[4] = new Point(2,0);
        A[5] = new Point(0,2);
        A[6] = new Point(0,-2);
        A[7] = new Point(-2,0);

        Point[] result = getConvexPoint(A);
        System.out.println("集合A中满足凸包的点集为：");
        for(int i = 0;i < result.length;i++)
            System.out.println("("+result[i].getX()+","+result[i].getY()+")");
    }
}

上面定义的点Point类代码如下：

package com.liuzhen.chapterThree;

public class Point {
    private int x;
    private int y;

    Point(){
        x = 0;
        y = 0;
    }

    Point(int x, int y){
        this.x = x;
        this.y = y;
    }

    public void setX(int x){
        this.x = x;
    }

    public int getX(){
        return x;
    }

    public void setY(int y){
        this.y = y;
    }

    public int getY(){
        return y;
    }
}

运行结果：

集合A中满足凸包的点集为：
(2,0)
(0,2)
(0,-2)
(-2,0)