Java实现有向图强连通分量的Tarjan算法

1 问题描述

引用自百度百科：

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

当DFN(u)=Low(u)时，以u为根的搜索子树上所有节点是一个强连通分量。

2 解决方案

下面代码所使用图：

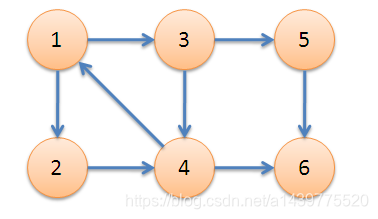
package com.liuzhen.practice;

import java.util.ArrayList;
import java.util.Scanner;
import java.util.Stack;

public class Main {
    public static int MAX = 100;
    public static int count;   //用于对图中顶点遍历的次序进行计数
    public static int n;
    public static int[] DFN = new int[MAX];    //记录图中每个节点的DFS遍历的时间戳(即次序)
    public static int[] Low = new int[MAX];   //记录每个顶点的所在树的根节点编号
    public static boolean[] inStack = new boolean[MAX];  //用于记录当前节点是否在栈中
    public static Stack<Integer> stack;

    public void init(int n) {
        count = 0;
        stack = new Stack<Integer>();
        for(int i = 0;i <= n;i++) {
            DFN[i] = -1;   //代表顶点i未被遍历
            Low[i] = -1;
            inStack[i] = false;
        }
    }

    static class edge {
        public int a;  //边的起点
        public int b;  //边的终点

        edge(int a, int b) {
            this.a = a;
            this.b = b;
        }
    }

    public void dfs(ArrayList<edge>[] map, int start) {
        DFN[start] = count++;
        Low[start] = DFN[start];
        stack.push(start);
        inStack[start] = true;
        int j = start;
        for(int i = 0;i < map[start].size();i++) {
            j = map[start].get(i).b;
            if(DFN[j] == -1) {  //顶点j未被遍历
                dfs(map, j);
                Low[start] = Math.min(Low[start], Low[j]);
            } else if(inStack[j]) {
                Low[start] = Math.min(Low[start], DFN[j]);
            }
        }
        if(DFN[start] == Low[start]) {
            System.out.print("强连通分量：");
             do {
                j = stack.pop();
                System.out.print(j+" ");
                inStack[j] = false;
            } while(start != j);
            System.out.println();
        }
        return;
    }

    public static void main(String[] args) {
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        test.init(n);
        int k = in.nextInt();  //有向图的边数目
        @SuppressWarnings("unchecked")
        ArrayList<edge>[] map = new ArrayList[n + 1];
        for(int i = 0;i <= n;i++)
            map[i] = new ArrayList<edge>();
        in.nextLine();
        for(int i = 0;i < k;i++) {
            int a = in.nextInt();
            int b = in.nextInt();
            map[a].add(new edge(a, b));
        }
        test.dfs(map, 1);
    }
}

运行结果：

8
2
3
4
4
5
1
6
6
强连通分量：6
强连通分量：5
强连通分量：3 4 2 1