Python 矩阵相关

　　Python 中矩阵运算主要使用numpy库。NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数索引的元素表格(通常是元素是数字）。因此对于随机查找来说，比python自带的list快很多。

　　在numpy里面通常使用两个变量：array和matrix。其实python标准类库中也有array，但是它的功能相对numpy的少很多，所以不用。matrix是array的分支，matrix可以看做二维的array，array可以是多维，matrix和array在很多时候都是通用的。官方建议如果两个都可以用，那就选择array，因为array更灵活，速度更快，很多人把二维的array也翻译成矩阵。但是matrix的优势在于，它相对于array使用的符号更简洁一些。

矩阵和向量的创建

　　a = np.array([2,4,5,6,7])

　　如上创建了一个1*5的一行5列的array，这就相当于一个行向量（实际上不是，应该用np.array([[2,4,5,6,7]])创建）。
　　m = np.matrix([[1,2,4,5,6],[5,6,8,9,4]])

　　如上创建了一个2*5的matrix，这就是一个2*5的矩阵。

　　另外矩阵还可以通过这个创建：
　　m = np.mat([[1,2,4,5,6],[5,6,8,9,4]])

　　mat和matrix的相关之处是，mat([])就等同于matrix([],copy=false)，而matrix([])实际上默认copy=true。

　　所以如果想引用一个矩阵，如m，可以使用a = mat(m)，或者a = matrix(m,copy=false)。当然用[]列表来新创建一个矩阵的时候它们是完全一样的。

矩阵的转置

　　m = m.transpose()

　　m = m.T

　　matrix和除一维外的array（甚至高维，尽管不清楚转置机制，但暂时用不上所以先不研究）可以通过这个两个进行转置（T和transpose不同点暂时不研究了）。

　　但是一维的array，它不是矩阵，也不是向量，所以不能通过transpose来转置。

　　因为在计算机里，二维和一维定义好以后就确定下来用几个索引标志来索引了。

　　而向量从功能上来看，应该被看做1行或1列的矩阵，所以它应该是二维的。就是说我们索引它的某个元素，比如行向量a的第3个元素，我们应该用a[1][3],而不是a[3]。

　　所以a = np.array([2,4,5,6,7])创建的其实啥也不是，像np.array([[2,4,5,6,7]])这样创建二维的才算真正意义上的行向量，也就能用transpose()来转置了。

　　如果用a = np.array([2,4,5,6,7,1,3,8])创建了一行数组a，想变成向量，就用reshape()函数来将它变成二维的向量。

reshape()函数

　　a = a.reshape([1,8])

　　把a转换为了二维的1行8列的行向量，即使a原来是一维数组。
　　a = a.reshape(8)

　　这样就又转回了原来一维的8元素的数组。　　　

　　甚至还可以a = a.reshape([2,2,2])

　　变成了2*2*2的三维的立方阵。

　　另外，如果赋值给一个新变量：

　　b = a.reshape([2,2,2])

　　a的shape没变，b是2*2*2的立方阵，而且它们共享内存，即a改变它的元素值，b也会改变。

矩阵乘法

　　乘法有三种表达方式：*、dot()、multiply()

np.multiply()

　　数组或矩阵的对应位置元素相乘。

np.dot()

　　对于一维数组array，执行对应位置相乘，然后再求和；对于秩不为1的二维数组（array）、矩阵（matrix），执行矩阵乘法运算（超过二维的可以参考numpy库介绍）

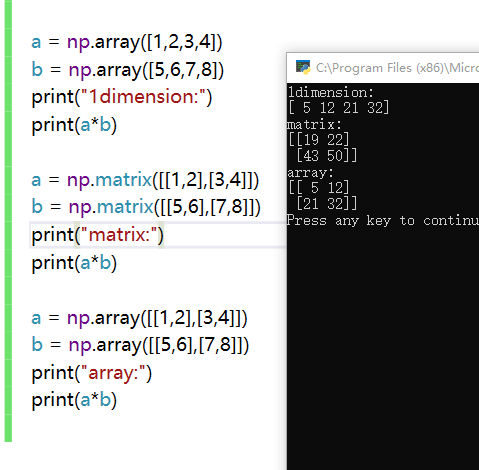
乘法运算*

　　对数组array执行对应位置元素相乘（相当于 np.multiply() 函数），对矩阵matrix执行矩阵乘法运算（相当于 np.dot() 函数）。就是multiply()和dot()的融合。

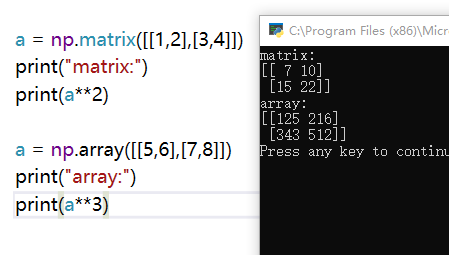
幂运算**

　　相当于多个array或matrix执行*，即A**3=A*A*A。

总结

　　multiply()全都是对应元素相乘；dot()是矩阵乘法，而一维array是对应元素相乘后之和；*对array是对应元素相乘，对matrix是矩阵乘法。

　　相对来说matrix注重矩阵操作，array注重阵列操作（阵中元素对应进行运算）