[Codeforces #615 div3]1294E Obtain a Permutation

Before the Beginniing

本文为 Clouder 原创文章，原文链接为Click，转载时请将本段放在文章开头显眼处。如进行了二次创作，请明确标明。

由本人转载于博客园。

题意分析

Codeforces题目链接

给出一个 $n \times m$ 的矩阵，给出两种操作：

将某一列整体向上移动一位。
修改某一个位置的值。

求最少要多少次操作，使得矩阵成为如下形式：

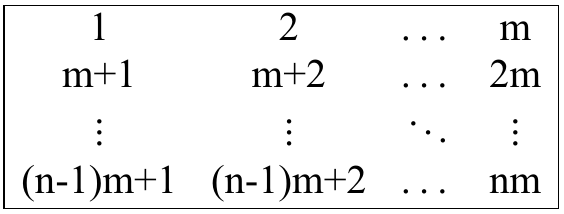
思路

很容易发现，每一列的操作都是独立的。

那么就一列列处理即可。

问题转化为如何求一列变为目标形式的最少操作次数。

而修改和平移是不冲突的，可以直接考虑先平移再修改。

暴力枚举法

于是得到一个很直观的思路，枚举向上移动多少次，再检查每一个数计算要修改多少次达到目标状态。

这样每列的复杂度是 $O(n^2)$ 的，总复杂度显然不可接受。

计算位置法

考虑每列要修改多少次受什么影响。

在向上平移特定距离之后，如果平移后有位置刚好对应上，则不需要修改。

每个位置数确定之后，其能对应的位置也确定了，可以直接计算出在平移几格时的情况该位置不需要修改。

比如图中第一列，第二行如果有一个数 $1$，可以直接通过计算得出其应当在的位置为第一行，于是在平移一格时的情况它不用修改，记录下来即可。

那么整体把矩阵扫一遍处理即可，时间复杂度 $O(nm)$，可以通过。

解法

还是有一些细节的。

首先不能直接开 $nm$ 大小的数组，会爆空间，这里使用了 vector 来处理。

而 $s[i]$ 代表的是向上平移 $i$ 格时有多少个位置不需要修改。

那么操作步数可以通过平移格数和修改数计算出。

这里的数组 $s$ 直接滚动优化掉一维，注意使用循环清空，就不会清空不使用的部分，而用 memset 会超时。

计算新位置建议自己画图手推一下，代个例子进去。

由于使用 vector，下标从 $0$ 开始了，按个人习惯来吧。

代码

#include <cstdio>

#include <vector>

using namespace std;

inline int read()

{

    static char c;

    int r = 0;

    for (c = getchar(); c > '9' || c < '0'; c = getchar());

    for (; c >= '0' && c <= '9'; r = (r << 1) + (r << 3) + (c ^ 48), c = getchar());

    return r;

}

const int maxn = 2e5 + 100;

int n, m;

vector<int> a[maxn];

int s[maxn];

int ans;

int main()

{

    n = read();

    m = read();

    for (int i = 0; i < n; ++i)

        for (int j = 0; j < m; ++j)

            a[i].push_back(read());

    int maxx = n * m;

    for (int j = 0; j < m; ++j)

    {

        for (int i = 0; i < n; ++i)

            s[i] = 0;

        for (int i = 0; i < n; ++i)

        {

            if (a[i][j] > maxx || a[i][j] < j || ((a[i][j] - j - 1) % m) != 0)

                continue;

            int p = (a[i][j] - j - 1) / m;

            if (i >= p)

                s[i - p]++;

            else

                s[i + n - p]++;

        }

        int res = 1 << 30;

        for (int i = 0; i < n; ++i)

            if (n - s[i] + i < res)

                res = n - s[i] + i;

        ans += res;

    }

    printf("%d\n", ans);

    return 0;

}