虚拟对抗训练（VAT）：一种用于监督学习和半监督学习的正则化方法

正则化

　　虚拟对抗训练是一种正则化方法，正则化在深度学习中是防止过拟合的一种方法。通常训练样本是有限的，而对于深度学习来说，搭设的深度网络是可以最大限度地拟合训练样本的分布的，从而导致模型与训练样本分布过分接近，还把训练样本中的一些噪声也拟合进去了，甚至于最极端的，训练出来的模型只能判断训练样本，而测试样本变成了随机判断。所以为了让模型泛化地更好，正则化是很有必要的。

　　最常见的正则化是直接对模型的参数的大小进行限制，比如将参数（整合为向量$\theta$）的$L_2$范数：

$\displaystyle J(\theta)=\frac{1}{n}\sum\limits_i^n\theta_i^2$

　　作为正则项加入损失函数中：

$\displaystyle L(\theta)=\frac{1}{N}\sum\limits_{i=1}^NL(y_i, x_i,\theta)  + \lambda J(\theta)$

　　从而约束参数不会很大而过于复杂，使模型符合奥卡姆剃刀原理：所有合适的模型中应该选择最简单的那个。

　　然而，这种正则化仅仅符合了奥卡姆剃刀而已，而且它的定义是很模糊的。因为你不知道什么模型才是“简单”的，而且仅仅用范数来限制也不一定就会产生“简单”的模型，甚至于，“简单”的模型也未必就是泛化能力强的模型。

对抗训练

　　相较于范数类型的正则项，论文中引用了另一篇论文，这篇论文从另一个角度来看待正则化，基于这样一个假设$A$：对于输入样本的微小变动，模型对它的预测输出也应该不会有很大的改变。这个对于连续函数来说是理所当然的（排除一些梯度特别大的连续函数），但是对于一些神经网络模型来说，它们内部层与层之间的交互是有阈值的，超过这个阈值才能把信息传到下一层，导致函数不连续，从而输入的微小改变就会对后面的输出产生巨大的影响（论文中指出，仅仅使用$L_p$范数做正则项就容易产生这样的问题）。它的正则项定义如下：

$\displaystyle J(\theta) = \frac{1}{N}\sum\limits_{i=1}^NL_{adv}(x_i,\theta)$

${\rm where}\,L_{adv}(x_i,\theta) = D[q(y|x_i),p(y|x_i+r_{adv_i},\theta)]$

${\rm where}\,r_{adv_i}= \mathop{\arg\max}\limits_{r;||r||_2\leq\epsilon}  D[q(y|x_i),p(y|x_i+r,\theta)]$

　　这个公式假设模型是生成模型，因为判别模型可以转化为生成模型，所以不另外添加公式了。其中，$D[q,p]$表示分布$q$和$p$的差异，用交叉熵、相对熵（KL散度）等表达；$q(y|x_i)$表示训练样本$x_i$的标签真实分布；$p(y|x_i,\theta)$表示模型参数为$\theta$时对$x_i$的标签预测分布；$r_{adv_i}$表示能使$x_i$预测偏差最大化的扰动向量（范数很小）。

　　因此，这个正则项的定义就是：在每一个训练样本点的周围（固定范围$\epsilon$），找一个预测分布和这个样本点标签的真实分布相差最大的样本点($x_i+r_{adv_i}$)，然后优化模型参数$\theta$来减小这个偏差。在每一次迭代优化$\theta$减小损失函数$L(\theta)$之前，都要先计算一次$r_{adv_i}$，即获取当前$\theta$下使每个$x_i$偏差最大的扰动向量，进而获取当前扰动的最大偏差作为正则项。如此看来好像是在对抗损失函数的减小，因此叫对抗训练，而 $r_{adv_i}$则叫对抗方向。

　　因为实际上样本点的真实连续分布并不能获得，所以使用离散的概率来作为分布，论文中使用one hot vector $h(y=y_{real})$来表达。这个向量是一串0-1编码，真实标签对应的向量元素为1，其它向量元素都为0，比如标签有：猫、狗、汽车，则$h(y = 狗)=[0,1,0]$，使用one hot vector的好处之一就是切断了不同标签之间在连续数值上的联系。

　　于是我们很容易能想到，对抗方向应该在$L_{adv}(x_i,\theta) $对$x_i$求梯度时能取到近似（因为在梯度方向函数变化率最大），即：

$\displaystyle r_{adv_i}\approx\epsilon\frac{g_i}{||g_i||_2},\,{\rm where}\,g_i=\nabla_{x}D[h(y=y_{x_i}),p(y|x,\theta)]|_{x=x_i}$

　　因为需要训练样本的真实标签分布，所以对抗训练只适用于监督学习。

　　论文指出，使用对抗方向来进行扰动的表现是比随机扰动要好的。随机扰动就是在$x_i$周围$\epsilon$内随机找一个较小的扰动$r_{rad_i}$代替$r_{adv_i}$。尽管随机扰动的目标也是假设A，但是最终的训练结果是比对抗扰动差很多的。

虚拟对抗训练

　　虚拟对抗训练（VAT Visual adversarial training）是基于对抗训练改进的正则化算法。它主要对对抗训练进行了两个地方的改进：

局部平滑度

　　在$L_{adv}(x_i,\theta)$定义中的标签真实分布$q(y|x_i)$被换成了当前迭代下的标签预测分布$p(y|x_i,\hat{\theta})$（$\hat{\theta}$表示当前梯度下降下的$\theta$的具体值，而$\theta$则是在损失函数中用来求梯度进行梯度下降的自变量）。另外还给$L_{adv}(x_i,\theta)$换了个名字——LDS（Local distributional smoothness 局部分布平滑度），定义如下：

${\rm LDS}(x_i,\theta) = D[p(y|x_i,\hat{\theta}),p(y|x_i+r_{vadv_i},\theta)]$

$\,{\rm where}\,r_{vadv_i}=\mathop{\arg\max}\limits_{r;||r||_2\leq\epsilon}  D[p(y|x_i,\hat{\theta}),p(y|x_i+r,\hat{\theta})]$

　　我们可能会疑惑，为什么计算$r_{vadv}$用$\hat{\theta}$，而不用$\theta$，明显用$\theta$更精确。论文中也没有给出明确的说明，可能它忘了说明这一点。不过这个细节也的确不容易察觉，在后面我会说一下我的理解。

　　可以发现，${\rm LDS}(x_i,\theta)$并不需要$x_i$的标签真实分布，所以即使$x_i$是没有真实标记的样本点，同样可以加入训练，因此VAT不但适用于监督学习，还适用于半监督学习。以下是使用VAT的简化的损失函数（$\mathcal{D_l,D_{ul}}$分别为有标记样本和无标记样本集）：

$\displaystyle L(\theta)=\sum\limits_{(x,y)\in\mathcal{D_l}}L(y, x,\theta) +\lambda \frac{1}{N_l+N_{ul}}\sum\limits_{x\in\mathcal{D_l,D_{ul}}}{\rm LDS}(x,\theta)$

快速计算$r_{vadv}$

　　对于计算$r_{vadv}$，论文并不直接使用关于$x_i$的梯度。因为显然$D[p(y|x_i,\hat{\theta}),p(y|x_i+r,\hat{\theta})]$在$r=0$时，两个分布完全相同，熵为0，如果可导，那么$x_i$就在极小值点上，从而梯度为0。于是论文换了一个思考角度，要求$D(r,x_i,\hat{\theta})$（简化写法）最大化，不一定只能从梯度的角度考虑。将它关于$r$在0处进行泰勒展开后，因为一阶导数（梯度）为0，发现有如下近似：

$\displaystyle D(r,x_i,\hat{\theta})\approx\frac{1}{2}r^THr+O(r^2)$

　　其中$O(r^2)$是$r^2$的高阶无穷小，$H=\nabla\nabla_rD(r,x_i,\hat{\theta})|_{r=0}$是Hessian矩阵。由Hessian矩阵的定义可知，该矩阵是实对称矩阵，一定有对应维数个相互线性无关的特征向量。由特征值和特征向量的定义得，对于范数大小固定的$r$，当$r$是最大特征值对应的特征向量时，能取得$r^THr$最大，又因为$r$的范数很小，后面的高阶无穷小可以忽略不计，相应地，$D(r,x_i,\hat{\theta})$也取得最大。所以：

$r_{vadv}\approx\mathop{\arg\max}\limits_{r;||r||_2\leq\epsilon}r^THr=\epsilon\overline{u}$

　　其中$\overline{u}$表示$H$的最大特征值对应的单位特征向量。但是，计算高维的Hessian矩阵是很困难的，更不用说再计算它的特征值和特征向量了。所以，论文使用幂法（幂迭代法，具体算法看此链接）来计算矩阵最大特征值对应的特征向量。即随机取一个同维度的向量$d$（假设用特征向量表达$d$时，$u$的系数不为0），进行以下迭代：

$d=\overline{Hd}$

　　迭代到后期，$d$会无限接近于$\overline{u}$。然后，论文又用所谓的有限差分法，来避免计算 Hessian矩阵。有限差分法就是用所谓的差商代替微商来近似计算导数，差商就是用比较小的因变量除以对应的自变量，微商就是用因变量的极限（无限小）除以对应自变量的极限。于是，0处的“二阶导数”$H$乘上一个较小的自变量$\xi d$，就可以近似0到$\xi d$处的一阶导数（梯度）的变化量：

$\xi Hd\approx\nabla_rD(r,x_i,\hat{\theta})|_{r=\xi d}-\nabla_rD(r,x_i,\hat{\theta})|_{r=0}$

　　由于$r=0$处的梯度为0：

$\displaystyle Hd\approx\frac{\nabla_rD(r,x_i,\hat{\theta})|_{r=\xi d}}{\xi}$

　　所以迭代式变为：

$d=\overline{\nabla_rD(r,x_i,\hat{\theta})|_{r=\xi d}}$

　　论文中实验，迭代一次就能获取很好的近似$u$的效果。即：

$\displaystyle r_{vadv}\approx\epsilon\frac{g}{||g||_2}$

${\rm where}\,g=\nabla_rD[p(y|x_i,\hat{\theta}),p(y|x_i+r,\hat{\theta})]|_{r=\xi d}$

　　我觉得迭代一次的原因应该是：相较迭代获取精度更高的虚拟对抗方向，计算力省下来用于梯度下降，更快地收敛整个模型更好。或者梯度下降前期迭代近似$r_{vadv}$次数少一些，后期再逐渐增加迭代次数增加收尾时的精度。

　　说一下我对为什么要用$\hat{\theta}$，而不用$\theta$的理解。因为需要计算$r=\xi d$处的梯度并进行迭代，如果使用不能当具体数值参与计算的参数$\theta$，就只能把整个迭代写成一次性计算的算式形式了，而且不能动态改变迭代的次数。并且随着迭代次数增多，参数$\theta$的数量会指数式上升。当然，如果和上面一样只迭代一次，我觉得是可以使用$\theta$的。不过论文第6页左上角好像说明了这点，当时没看懂，说的应该就是这个意思：

额外正则项

　　另外，在实验中，论文除了LDS正则项外，还添加了条件熵作为额外的正则项。定义如下：

$\displaystyle\mathcal{H}(Y|X)=-\frac{1}{N_l+N_{ul}}\sum\limits_{x\in \mathcal{D_l,D_{ul}}}\sum\limits_{y}p(y|x,\theta)\log p(y|x,\theta)$

　　表示除了相似输入应该有相似输出外（减小LDS），输出标签的概率分布还应该越集中越好（减小$\mathcal{H}(Y|X)$）。因为在$X$条件下$Y$的混乱度（熵）代表了输出概率分布的不集中度的平均值，所以优化条件熵越小，输出概率分布越集中、越确定。而预测地越明确越好自然是我们想要的。

VAT效果

　　下图展示了使用VAT进行半监督训练的过程：

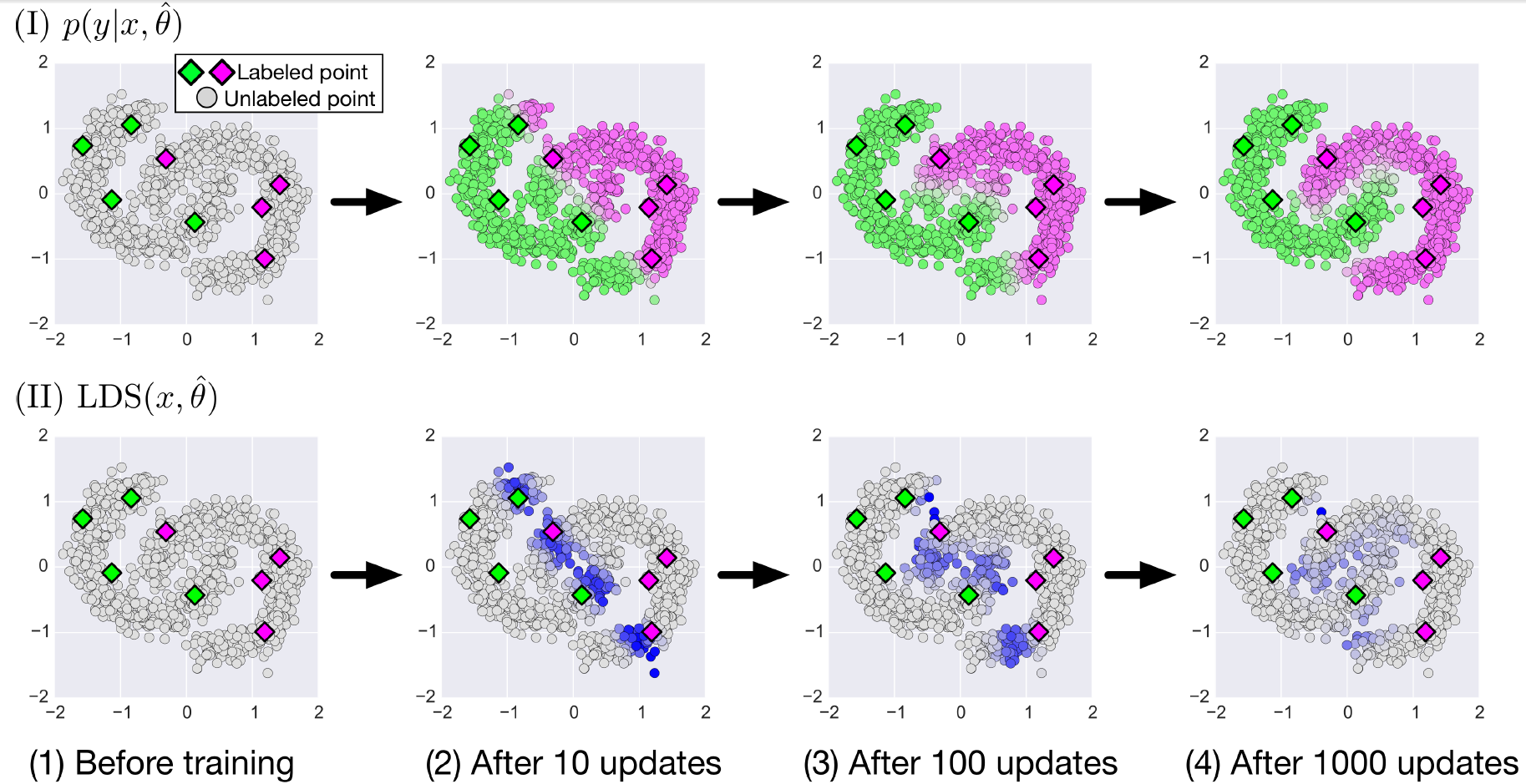
　　图中方形图标是有标签训练样本，圆形图标是无标签训练样本。分成上下两部分，分别展示了在训练之前、训练更新（梯度下降）10次、100次、1000次时，模型对无标签训练样本的预测情况$({\rm I})$，和无标签训练样本的LDS$({\rm II})$。样本的输入为二维，分别用横纵坐标表示。模型预测输出为一维，从绿到灰，再到紫，用连续的颜色过渡来表示预测标签为某个类别的概率（紫色概率为1，绿色概率为0，灰色为0.5），如$({\rm I})$所示。$({\rm II})$用灰色到紫色表示无标签样本的LDS大小，越紫说明该样本点在当前模型下的LDS越大，说明对这个样本点进行小扰动会使当前模型的预测出现大偏差。

　　$({\rm I})$可以看出，随着不断的更新，无标签样本的预测从有标签样本“传染”出去（因为遵循相近的样本预测相同的理念），直到停在无标签样本稀疏的地方（因为没有样本再进行减小LDS的“传染”，而稀疏的地方也正好就是两个类别的分界线），最终形成了两个镶嵌着的半圆环。这个“传染”的效果是我之前没想到的，我以为减小LDS的效果仅仅局限在有标签样本的周围。但是加了大量的无标签样本后，这些样本对模型进行了总体的“把控”，而少量的有标签样本则对这个总体进行了“固定”，二者联动，使得VAT半监督学习的学习效果很好。

　　$({\rm II})$显示LDS随着模型的更新，越来越小，最后LDS较大大的样本点都分布在两个标签的分界线处。

论文信息

　　Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning