题目

A graph which is connected and acyclic can be considered a tree. The height of the tree depends on the selected root. Now you are supposed to find the root that results in a highest tree. Such a root is called the deepest root.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (<=10000) which is the number of nodes, and hence the nodes are numbered from 1 to N. Then N-1 lines follow, each describes an edge by given the two adjacent nodes’ numbers.

Output Specification:

For each test case, print each of the deepest roots in a line. If such a root is not unique, print them in increasing order of their numbers. In case that the given graph is not a tree, print “Error: K components” where K is the number of connected components in the graph.

Sample Input 1:

5

1 2

1 3

1 4

2 5

Sample Output 1:

3

4

5

Sample Input 2:

5

1 3

1 4

2 5

3 4

Sample Output 2:

Error: 2 components

题目分析

已知图的顶点N和边N-1，判断所给图是否是一棵树，如果是，查找并打印最高树的所有根节点（从小到大）

  • 判断图为树有两个条件：只有一个连通分量（否则为森林）；无环（已知顶点数为N，边为N-1的连通图一定是树）
  • 最高树的所有根节点，其含义可以从样例中推导得出（起始顶点不同，寻找出的最高树不同）

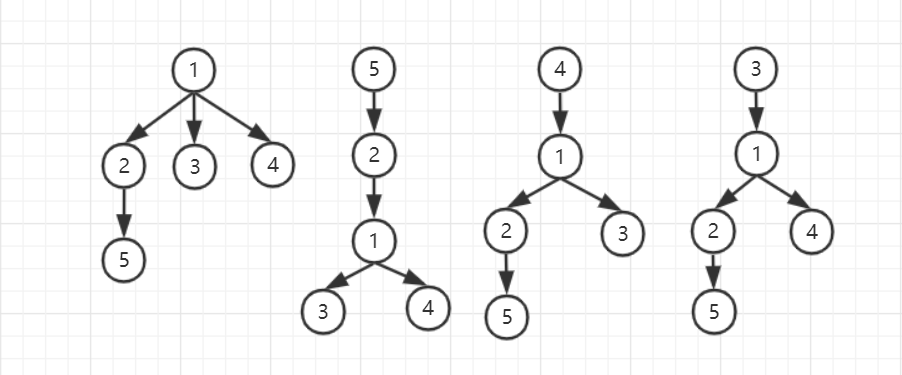
解题思路

1. 存储顶点和边

  • 邻接表
  • 邻接矩阵

2. 计算连通分量个数

连通分量等于1时，满足条件

  • DFS
  • BFS
  • 并查集

3. 查找最大高度树的根节点

  • 任意取一个顶点，求其能到达的最远的节点集合A，如测试样例1中：取1，可以得到5,3,4
  • 任取取A集合中一个顶点，求其能到达的最远的节点集合B，如取A集合中3，可以得到4,5
  • 集合A和集合B的并集去重排序，即为答案

Code

Code 01（邻接矩阵 并查集）

  1. #include <iostream>
  2. #include <vector>
  3. #include <set>
  4. using namespace std;
  5. const int maxn=10010;
  6. vector<int> g[maxn],temp; //邻接表 存储边
  7. set<int> vs; // 存储所有满足条件的 the deepest roots
  8. int maxh,n,father[maxn],vis[maxn];
  9. /*
  10. 	并查集判断连通分量树
  11. 	两次dfs求the deepest root
  12. */
  13. int init() { /* 并查集 初始化 */
  14. 	for(int i=1; i<=n; i++)father[i]=i;
  15. }
  16. int find(int x) { /* 并查集 查 */
  17. 	int a = x;
  18. 	while(x!=father[x]) {
  19. 		x=father[x];
  20. 	}
  21. 	while(a!=father[a]) { // 路径压缩
  22. 		int temp=a;
  23. 		a=father[a];
  24. 		father[a]=x;
  25. 	}
  26. 	return x;
  27. }
  28. void Union(int a,int b) { /* 并查集 并 */
  29. 	int fa=find(a);
  30. 	int fb=find(b);
  31. 	if(fa<fb)father[fb]=fa;
  32. 	else father[fa]=fb;
  33. }
  34. void dfs(int a, int h) { /* dfs */
  35. 	vis[a]=1;
  36. 	if(h>maxh) {
  37. 		temp.clear();
  38. 		temp.push_back(a); // the deepest root
  39. 		maxh=h;
  40. 	} else if(h==maxh)
  41. 		temp.push_back(a);
  42. 	for(int i=0; i<g[a].size(); i++) {
  43. 		if(vis[g[a][i]]==0)
  44. 			dfs(g[a][i],h+1);
  45. 	}
  46. }
  47. void pts() {
  48. 	for(int i=0; i<temp.size(); i++)
  49. 		vs.insert(temp[i]);
  50. }
  51. int main(int argc,char * argv[]) {
  52. 	int a,b;
  53. 	scanf("%d",&n);
  54. 	init();
  55. 	for(int i=1; i<=n-1; i++) {
  56. 		scanf("%d %d",&a,&b);
  57. 		g[a].push_back(b);
  58. 		g[b].push_back(a);
  59. 		Union(a,b);
  60. 	}
  61. 	// 统计连通分量数
  62. 	for(int i=1; i<=n; i++) {
  63. 		vs.insert(find(i));
  64. 	}
  65. 	if(vs.size()>1) {
  66. 		printf("Error: %d components",vs.size());
  67. 		return 0;
  68. 	}
  69. 	vs.clear(); //vs重置，方便下面使用
  70. 	dfs(1,1); // 第一次dfs，任意取一个顶点，获取最深根集合A
  71. 	pts(); //将集合A存入set
  72. 	fill(vis,vis+maxn,0); //重置vis访问标记数组
  73. 	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
  74. 	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
  75. 	pts(); //将集合B存入set
  76. 	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
  77. 		printf("%d\n",*it);
  78. 	}
  79. 	return 0;
  80. }

Code 02（邻接矩阵 DFS）

  1. #include <iostream>
  2. #include <vector>
  3. #include <set>
  4. using namespace std;
  5. const int maxn=10010;
  6. vector<int> g[maxn],temp; //邻接表 存储边
  7. set<int> vs; // 存储所有满足条件的 the deepest roots
  8. int n,maxh,vis[maxn];
  9. /*
  10. 	第一次dfs 求连通分量，求the deepest root集合A
  11. 	第二次dfs 求the deepest root集合B
  12. 	集合A+B，去重排序 即为答案
  13. */
  14. void dfs(int a, int h) { /* dfs */
  15. 	vis[a]=1;
  16. 	if(h>maxh) {
  17. 		temp.clear();
  18. 		temp.push_back(a); // the deepest root
  19. 		maxh=h;
  20. 	} else if(h==maxh)
  21. 		temp.push_back(a);
  22. 	for(int i=0; i<g[a].size(); i++) {
  23. 		if(vis[g[a][i]]==0)
  24. 			dfs(g[a][i],h+1);
  25. 	}
  26. }
  27. void pts() {
  28. 	for(int i=0; i<temp.size(); i++)
  29. 		vs.insert(temp[i]);
  30. }
  31. int main(int argc,char * argv[]) {
  32. 	int a,b;
  33. 	scanf("%d",&n);
  34. 	for(int i=1; i<=n-1; i++) {
  35. 		scanf("%d %d",&a,&b);
  36. 		g[a].push_back(b);
  37. 		g[b].push_back(a);
  38. 	}
  39. 	// 统计连通分量数
  40. 	int cnt=0;
  41. 	for(int i=1; i<=n; i++) {
  42. 		if(vis[i]==0){
  43. 			dfs(i,0);
  44. 			pts(); //将集合A存入set
  45. 			cnt++;
  46. 		}
  47. 	}
  48. 	if(cnt>1) {
  49. 		printf("Error: %d components",cnt);
  50. 		return 0;
  51. 	}
  52. 	fill(vis,vis+maxn,0); //重置vis访问标记数组
  53. 	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
  54. 	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
  55. 	pts(); //将集合B存入set
  56. 	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
  57. 		printf("%d\n",*it);
  58. 	}
  59. 	return 0;
  60. }

Code 03（邻接矩阵 BFS）

  1. #include <iostream>
  2. #include <vector>
  3. #include <set>
  4. #include <queue>
  5. using namespace std;
  6. const int maxn=10010;
  7. vector<int> g[maxn],temp; //邻接表 存储边
  8. set<int> vs; // 存储所有满足条件的 the deepest roots
  9. int n,maxh,vis[maxn];
  10. struct node {
  11. 	int v;
  12. 	int h;
  13. };
  14. /*
  15. 	第一次bfs 求连通分量，求the deepest root集合A
  16. 	第二次bfs 求the deepest root集合B
  17. 	集合A+B，去重排序 即为答案
  18. */
  19. void bfs(int a) { /* dfs */
  20. 	vis[a]=1;
  21. 	queue<node> q;
  22. 	q.push({a,0});
  23. 	while(!q.empty()) {
  24. 		node now = q.front();
  25. 		q.pop();
  26. 		if(now.h>maxh) {
  27. 			temp.clear();
  28. 			temp.push_back(now.v); // the deepest root
  29. 			maxh=now.h;
  30. 		} else if(now.h==maxh)
  31. 			temp.push_back(now.v);
  32. 		for(int i=0; i<g[now.v].size(); i++)
  33. 			if(vis[g[now.v][i]]==0){
  34. 				q.push({g[now.v][i],now.h+1});
  35. 				vis[g[now.v][i]]=1;
  36. 			}
  37. 	}
  38. }
  39. void pts() {
  40. 	for(int i=0; i<temp.size(); i++)
  41. 		vs.insert(temp[i]);
  42. }
  43. int main(int argc,char * argv[]) {
  44. 	int a,b;
  45. 	scanf("%d",&n);
  46. 	for(int i=1; i<=n-1; i++) {
  47. 		scanf("%d %d",&a,&b);
  48. 		g[a].push_back(b);
  49. 		g[b].push_back(a);
  50. 	}
  51. 	// 统计连通分量数
  52. 	int cnt=0;
  53. 	for(int i=1; i<=n; i++) {
  54. 		if(vis[i]==0) {
  55. 			bfs(i);
  56. 			pts(); //将集合A存入set
  57. 			cnt++;
  58. 		}
  59. 	}
  60. 	if(cnt>1) {
  61. 		printf("Error: %d components",cnt);
  62. 		return 0;
  63. 	}
  64. 	fill(vis,vis+maxn,0); //重置vis访问标记数组
  65. 	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
  66. 	bfs(temp[0]);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
  67. 	pts(); //将集合B存入set
  68. 	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++)  //set默认从小到大，A+B去重即为结果
  69. 		printf("%d\n",*it);
  70. 	return 0;
  71. }

Code 04（邻接表 DFS）

  1. #include <iostream>
  2. #include <vector>
  3. #include <set>
  4. using namespace std;
  5. const int maxn=10010;
  6. vector<int> temp; //邻接表 存储边
  7. set<int> vs; // 存储所有满足条件的 the deepest roots
  8. int n,maxh,vis[maxn],g[maxn][maxn];
  9. /*
  10. 	第一次dfs 求连通分量，求the deepest root集合A
  11. 	第二次dfs 求the deepest root集合B
  12. 	集合A+B，去重排序 即为答案
  13. */
  14. void dfs(int a, int h) { /* dfs */
  15. 	vis[a]=1;
  16. 	if(h>maxh) {
  17. 		temp.clear();
  18. 		temp.push_back(a); // the deepest root
  19. 		maxh=h;
  20. 	} else if(h==maxh)
  21. 		temp.push_back(a);
  22. 	for(int i=1; i<maxn; i++)
  23. 		if(g[a][i]==1 && vis[i]==0)
  24. 			dfs(i,h+1);
  25. }
  26. void pts() {
  27. 	for(int i=0; i<temp.size(); i++)
  28. 		vs.insert(temp[i]);
  29. }
  30. int main(int argc,char * argv[]) {
  31. 	int a,b;
  32. 	scanf("%d",&n);
  33. 	for(int i=1; i<=n-1; i++) {
  34. 		scanf("%d %d",&a,&b);
  35. 		g[a][b]=1;
  36. 		g[b][a]=1;
  37. 	}
  38. 	// 统计连通分量数
  39. 	int cnt=0;
  40. 	for(int i=1; i<=n; i++) {
  41. 		if(vis[i]==0) {
  42. 			dfs(i,0);
  43. 			pts(); //将集合A存入set
  44. 			cnt++;
  45. 		}
  46. 	}
  47. 	if(cnt>1) {
  48. 		printf("Error: %d components",cnt);
  49. 		return 0;
  50. 	}
  51. 	fill(vis,vis+maxn,0); //重置vis访问标记数组
  52. 	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
  53. 	dfs(temp[0],1);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
  54. 	pts(); //将集合B存入set
  55. 	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++) { //set默认从小到大，A+B去重即为结果
  56. 		printf("%d\n",*it);
  57. 	}
  58. 	return 0;
  59. }

Code 05（邻接表 BFS）

  1. #include <iostream>
  2. #include <vector>
  3. #include <set>
  4. #include <queue>
  5. using namespace std;
  6. const int maxn=10010;
  7. vector<int> temp; //邻接表 存储边
  8. set<int> vs; // 存储所有满足条件的 the deepest roots
  9. int n,maxh,vis[maxn],g[maxn][maxn];
  10. struct node {
  11. 	int v;
  12. 	int h;
  13. };
  14. /*
  15. 	第一次bfs 求连通分量，求the deepest root集合A
  16. 	第二次bfs 求the deepest root集合B
  17. 	集合A+B，去重排序 即为答案
  18. */
  19. void bfs(int a) { /* dfs */
  20. 	vis[a]=1;
  21. 	queue<node> q;
  22. 	q.push({a,0});
  23. 	while(!q.empty()) {
  24. 		node now = q.front();
  25. 		q.pop();
  26. 		if(now.h>maxh) {
  27. 			temp.clear();
  28. 			temp.push_back(now.v); // the deepest root
  29. 			maxh=now.h;
  30. 		} else if(now.h==maxh)
  31. 			temp.push_back(now.v);
  32. 		for(int i=1; i<maxn; i++)
  33. 			if(g[now.v][i]==1 && vis[i]==0){
  34. 				q.push({i,now.h+1});
  35. 				vis[i]=1;
  36. 			}
  37. 	}
  38. }
  39. void pts() {
  40. 	for(int i=0; i<temp.size(); i++)
  41. 		vs.insert(temp[i]);
  42. }
  43. int main(int argc,char * argv[]) {
  44. 	int a,b;
  45. 	scanf("%d",&n);
  46. 	for(int i=1; i<=n-1; i++) {
  47. 		scanf("%d %d",&a,&b);
  48. 		g[a][b]=1;
  49. 		g[b][a]=1;
  50. 	}
  51. 	// 统计连通分量数
  52. 	int cnt=0;
  53. 	for(int i=1; i<=n; i++) {
  54. 		if(vis[i]==0) {
  55. 			bfs(i);
  56. 			pts(); //将集合A存入set
  57. 			cnt++;
  58. 		}
  59. 	}
  60. 	if(cnt>1) {
  61. 		printf("Error: %d components",cnt);
  62. 		return 0;
  63. 	}
  64. 	fill(vis,vis+maxn,0); //重置vis访问标记数组
  65. 	//maxh=0; //无需重置maxh，因为第一轮得到的maxh即为最高树高度，第二轮中h==maxh时添加剩余的the deepest root
  66. 	bfs(temp[0]);// 第二次dfs，从集合A中任取一个顶点，获取最深根集合B
  67. 	pts(); //将集合B存入set
  68. 	for(set<int>::iterator it=vs.begin(); it!=vs.end(); it++)  //set默认从小到大，A+B去重即为结果
  69. 		printf("%d\n",*it);
  70. 	return 0;
  71. }

PAT Advanced A1021 Deepest Root (25) [图的遍历，DFS，计算连通分量的个数，BFS，并查集]的更多相关文章

  1. PAT Advanced 1013 Battle Over Cities (25) [图的遍历，统计连通分量的个数，DFS，BFS，并查集]

    题目 It is vitally important to have all the cities connected by highways in a war. If a city is occup ...

  2. PAT 甲级 1021 Deepest Root (25 分)（bfs求树高,又可能存在part数part>2的情况）

    1021 Deepest Root (25 分)   A graph which is connected and acyclic can be considered a tree. The heig ...

  3. PAT甲级——A1021 Deepest Root

    A graph which is connected and acyclic can be considered a tree. The height of the tree depends on t ...

  4. PAT Advanced 1020 Tree Traversals (25) [⼆叉树的遍历，后序中序转层序]

    题目 Suppose that all the keys in a binary tree are distinct positive integers. Given the postorder an ...

  5. PAT Advanced 1138 Postorder Traversal (25) [树的遍历，前序中序转后序]

    题目 Suppose that all the keys in a binary tree are distinct positive integers. Given the preorder and ...

  6. [PAT] 1021 Deepest Root (25)（25 分）

    1021 Deepest Root (25)(25 分)A graph which is connected and acyclic can be considered a tree. The hei ...

  7. PAT甲级1021. Deepest Root

    PAT甲级1021. Deepest Root 题意: 连接和非循环的图可以被认为是一棵树.树的高度取决于所选的根.现在你应该找到导致最高树的根.这样的根称为最深根. 输入规格: 每个输入文件包含一个 ...

  8. PAT 甲级 1021 Deepest Root (并查集，树的遍历)

    1021. Deepest Root (25) 时间限制 1500 ms 内存限制 65536 kB 代码长度限制 16000 B 判题程序 Standard 作者 CHEN, Yue A graph ...

  9. 图的遍历DFS

    图的遍历DFS 与树的深度优先遍历之间的联系 树的深度优先遍历分为:先根,后根 //树的先根遍历 void PreOrder(TreeNode *R){ if(R!=NULL){ visit(R); ...

随机推荐

  1. JuJu团队1月7号工作汇报

    JuJu团队1月7号工作汇报 JuJu 周六周日放假,所以空了两天~   Scrum 团队成员 今日工作 剩余任务 困难 飞飞 完成data process readme部分 实现三维Dense 无 ...

  2. windows环境批量更改文件名

    1.打开命令提示符,进入需更新文件所在的目录下(不熟悉的参考:https://blog.csdn.net/u012995964/article/details/53119516)2.批量命名      ...

  3. CodeForces - 869B The Eternal Immortality

    题意:已知a,b,求的最后一位. 分析: 1.若b-a>=5,则尾数一定为0,因为连续5个数的尾数要么同时包括一个5和一个偶数,要么包括一个0. 2.若b-a<5,直接暴力求即可. #in ...

  4. MySQL 如何使用 PV 和 PVC？【转】

    本节演示如何为 MySQL 数据库提供持久化存储,步骤为: 创建 PV 和 PVC. 部署 MySQL. 向 MySQL 添加数据. 模拟节点宕机故障,Kubernetes 将 MySQL 自动迁移到 ...

  5. centos 7安装nodejs

    ps: {install_path} 安装目录路径 1.安装wget yum install wget 2. 下载对应文件 wget -c https://nodejs.org/dist/v8.9.1 ...

  6. R 对数变换 《回归分析与线性统计模型》page103

    BG:在box-cox变换中,当λ = 0时即为对数变换. 当所分析变量的标准差相对于均值而言比较大时,这种变换特别有用.对数据作对数变换常常起到降低数据波动性和减少不对称性的作用..这一变换也能有效 ...

  7. Day4 - M - Roads in Berland CodeForces - 25C

    There are n cities numbered from 1 to n in Berland. Some of them are connected by two-way roads. Eac ...

  8. 把自己的项目发布到maven仓库并在maven和gradle中开始使用

    把自己的项目发布到maven仓库并在maven和gradle中开始使用 上一条博客中提到的日志打印项目总算是维护的差不多了, 不过现在使用它还是打成jar包放到其他项目内, 所以决定把项目传到mave ...

  9. 使用conda创建虚拟环境

    conda创建python虚拟环境 前言 conda常用的命令: conda list 查看安装了哪些包. conda env list 或 conda info -e 查看当前存在哪些虚拟环境 co ...

  10. [题解] LuoguP2257 YY的GCD

    传送门 给\(n,m\),让你求 \[ \sum\limits_{i=1}^n \sum\limits_{j=1}^m [\gcd(i,j) \in prime] \] 有\(T\)组询问\((T \ ...