[最短路,floyd] Codeforces 1204C Anna, Svyatoslav and Maps

题目:http://codeforces.com/contest/1204/problem/C

C. Anna, Svyatoslav and Maps

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The main characters have been omitted to be short.

You are given a directed unweighted graph without loops with nn vertexes and a path in it (that path is not necessary simple) given by a sequence p1,p2,…,pmp1,p2,…,pm of mm vertexes; for each 1≤i<m1≤i<m there is an arc from pipi to pi+1pi+1.

Define the sequence v1,v2,…,vkv1,v2,…,vk of kk vertexes as good, if vv is a subsequence of pp, v1=p1v1=p1, vk=pmvk=pm, and pp is one of the shortest paths passing through the vertexes v1v1, ……, vkvk in that order.

A sequence aa is a subsequence of a sequence bb if aa can be obtained from bb by deletion of several (possibly, zero or all) elements. It is obvious that the sequence pp is good but your task is to find the shortest good subsequence.

If there are multiple shortest good subsequences, output any of them.

Input

The first line contains a single integer nn (2≤n≤1002≤n≤100) — the number of vertexes in a graph.

The next nn lines define the graph by an adjacency matrix: the jj-th character in the ii-st line is equal to 11 if there is an arc from vertex ii to the vertex jj else it is equal to 00. It is guaranteed that the graph doesn't contain loops.

The next line contains a single integer mm (2≤m≤1062≤m≤106) — the number of vertexes in the path.

The next line contains mm integers p1,p2,…,pmp1,p2,…,pm (1≤pi≤n1≤pi≤n) — the sequence of vertexes in the path. It is guaranteed that for any 1≤i<m1≤i<m there is an arc from pipi to pi+1pi+1.

Output

In the first line output a single integer kk (2≤k≤m2≤k≤m) — the length of the shortest good subsequence. In the second line output kk integers v1v1, ……, vkvk (1≤vi≤n1≤vi≤n) — the vertexes in the subsequence. If there are multiple shortest subsequences, print any. Any two consecutive numbers should be distinct.

Examples

input

Copy

output

Copy

3

1 2 4

input

Copy

4

0110

0010

1001

1000

20

1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4

output

Copy

11

1 2 4 2 4 2 4 2 4 2 4

input

Copy

3

011

101

110

7

1 2 3 1 3 2 1

output

Copy

7

1 2 3 1 3 2 1

input

Copy

output

Copy

2

1 4

Note

Below you can see the graph from the first example:

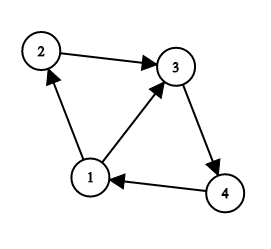
The given path is passing through vertexes 11, 22, 33, 44. The sequence 1−2−41−2−4 is good because it is the subsequence of the given path, its first and the last elements are equal to the first and the last elements of the given path respectively, and the shortest path passing through vertexes 11, 22 and 44 in that order is 1−2−3−41−2−3−4. Note that subsequences 1−41−4 and 1−3−41−3−4 aren't good because in both cases the shortest path passing through the vertexes of these sequences is 1−3−41−3−4.

In the third example, the graph is full so any sequence of vertexes in which any two consecutive elements are distinct defines a path consisting of the same number of vertexes.

In the fourth example, the paths 1−2−41−2−4 and 1−3−41−3−4 are the shortest paths passing through the vertexes 11 and 44.

题意:

给出n个点和他们的邻接关系,再给出一个序列,问如何删去尽可能多的点使得剩下的点的最短路仍是原序列

思路:

如果当前点到当前遍历到的点的距离大于最短路,则说明当前点是必须被加进答案的,因为要保证最短路是给出的序列,如果不选这个点就会让序列最短路变短,
所以更新答案的当前节点为遍历到的节点的上一个节点,当前节点到遍历的点的最短距离也要更新
比如样例1中原序列为1 2 3 4,其中1->2->3距离为2,而1->3的最短路为1,所以我们要加入2节点才能保证最短路仍是原来的序列,否则最短路就会变短

 #include<bits/stdc++.h>

 using namespace std;

 const int amn=1e2+,amn1=1e6+,inf=0x3f3f3f3f;

 int dis[amn][amn],a[amn][amn],p[amn1],ans[amn1];

 int main(){

     int n,m;char in;

     ios::sync_with_stdio();

     cin>>n;

     for(int i=;i<=n;i++){

         for(int j=;j<=n;j++){

             cin>>in;

             a[i][j]=in-'';

             if(i==j)dis[i][j]=;

             else{

                 if(a[i][j])dis[i][j]=;

                 else dis[i][j]=inf;

             }

         }

     }

     ///floyd求任意两点间的最短路

     for(int k=;k<=n;k++)

         for(int i=;i<=n;i++)

             for(int j=;j<=n;j++)

                 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

     cin>>m;

     for(int i=;i<=m;i++)cin>>p[i];

     int d=,tp=;   ///d为当前点到当前遍历到的点的距离

     ans[++tp]=p[]; ///题目要求开头必须在序列中

     for(int i=;i<=m;i++){

         d+=dis[p[i-]][p[i]];

         if(d<=dis[ans[tp]][p[i]])continue;

         ans[++tp]=p[i-];   ///如果当前点到当前遍历到的点的距离大于最短路,则说明当前点是必须被加进答案的,因为要保证最短路是给出的序列,如果不选这个点就会让最短路变短,所以更新答案的当前节点,当前节点到遍历的点的最短距离也要更新

         d=dis[ans[tp]][p[i]];

     }

     ans[++tp]=p[m]; ///题目要求结尾必须在序列中

     printf("%d\n",tp);

     for(int i=;i<=tp;i++)printf("%d%c",ans[i],i<tp?' ':'\n');

 }

 /**

 给出n个点和他们的邻接关系,再给出一个序列,问如何删去尽可能多的点使得剩下的点的最短路仍是原序列

 如果当前点到当前遍历到的点的距离大于最短路,则说明当前点是必须被加进答案的,因为要保证最短路是给出的序列,如果不选这个点就会让序列最短路变短,

 所以更新答案的当前节点为遍历到的节点的上一个节点,当前节点到遍历的点的最短距离也要更新

 比如样例1中原序列为1 2 3 4,其中1->2->3距离为2,而1->3的最短路为1,所以我们要加入2节点才能保证最短路仍是原来的序列,否则最短路就会变短

 **/