POJ 3013 SPFA算法，邻接表的使用

Big Christmas Tree

Time Limit: 3000MS		Memory Limit: 131072K
Total Submissions: 19029		Accepted: 4058

Description

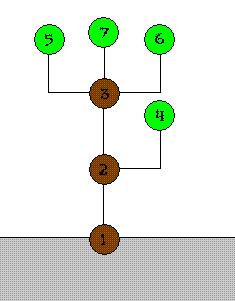Christmas is coming to KCM city. Suby the loyal civilian in KCM city is preparing a big neat Christmas tree. The simple structure of the tree is shown in right picture.

The tree can be represented as a collection of numbered nodes and some edges. The nodes are numbered 1 through n. The root is always numbered 1. Every node in the tree has its weight. The weights can be different from each other. Also the shape of every available edge between two nodes is different, so the unit price of each edge is different. Because of a technical difficulty, price of an edge will be (sum of weights of all descendant nodes) × (unit price of the edge).

Suby wants to minimize the cost of whole tree among all possible choices. Also he wants to use all nodes because he wants a large tree. So he decided to ask you for helping solve this task by find the minimum cost.

Input

The input consists of T test cases. The number of test cases T is given in the first line of the input file. Each test case consists of several lines. Two numbers v, e (0 ≤v, e ≤ 50000) are given in the first line of each test case. On the next line, v positive integers w_i indicating the weights of v nodes are given in one line. On the following e lines, each line contain three positive integers a, b, c indicating the edge which is able to connect two nodes a and b, and unit price c.

All numbers in input are less than 2¹⁶.

Output

For each test case, output an integer indicating the minimum possible cost for the tree in one line. If there is no way to build a Christmas tree, print “No Answer” in one line.

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

学习了一下SPFA算法，咋一看去以为这个题目是最小生成树，但是题目条件边的权值由子节点的点值和决定，这个就很纠结了，。。。在建树过程中，还要一边求某边的子节点，不是很蛋疼吗。。。后来大牛们都说是SPFA最短路求。。。推了一下，发现真是，当求出了源点1到各节点的最短路，再乘以节点值，再累加，就奇迹般的达到了上述效果

最短路就是用SPFA实现的，为了运用SPFA算法，首先还得学会使用邻接表。
邻接表和邻接矩阵的思想相反，邻接表存贮边信息，运用链表的思想将读入的所有边都存在一个链表中、
邻接表的实现是这样的，
for 1 to m 
scanf a,b,c
u[i]=a,v[i]=b,w[i]=c;
next[i]=first[u[i]];
first[u[i]]=i;
稍微递推一下，发现，这链表是自尾向前链接的，主要就是它的next放在first前面，first里面保存u[i]节点是第几条边，初始化first数组全部为-1，这也就不难理解，如果u[i]是第一次读入，那next[i]值为-1，表示下面没有跟u[i]再相邻的未访问边了，而first数组的存在使得如果再次读入u[i]为初始节点，则马上更新。。到时候访问的时候实际上是从最新读入的边访问到最底层的边，有点类似于后进先出的栈的味道

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define maxn 50005
#define inf 0x7fffffffffffffff
using namespace std;

int v[maxn*];
int u[maxn*];
int w[maxn*];
int pre[maxn*];
int next[maxn*];
long long d[maxn];
int vn[maxn];
bool isqueue[maxn];
void init(int n)
{
    for (int i=;i<=n;i++)
    {
        d[i]=inf;
        isqueue[i]=;
    }
    memset(pre,-,sizeof pre); //初始化邻接表的数组全为-1
}
int cnt;
void addedge(int be,int de,int ve) //建立邻接表
{
    u[cnt]=be;
    v[cnt]=de;
    w[cnt]=ve;
    next[cnt]=pre[be];
    pre[be]=cnt++;
}
int main()
{
     int t;
     scanf("%d",&t);
     while (t--)
     {
         int n,m;
         scanf("%d %d",&n,&m);
         init(n);
         int i,j,k;
         for (i=;i<=n;i++)
         {
             scanf("%d",&vn[i]);
         }
         cnt=;
         for (j=;j<=m;j++)
         {
             int a,b,c;
             scanf("%d %d %d",&a,&b,&c);
             addedge(a,b,c);
             addedge(b,a,c);
         }
         d[]=;
         queue<int> q;
         q.push();
         isqueue[]=;
         while (!q.empty())//SPFA通过队列来实现
         {
             int vs=q.front();
             q.pop();
             isqueue[vs]=;
             for (int qq=pre[vs];qq>=;qq=next[qq]) //访问与该节点相连的各条边，直至-1，即没有了边
             {

                 if (d[v[qq]]>d[vs]+w[qq])
                 {
                   d[v[qq]]=d[vs]+w[qq];//将新点存入队列。
                   if (!isqueue[v[qq]])
                    {
                     q.push(v[qq]);
                     isqueue[v[qq]]=;
                    }

                 }
             }
         }//循环结束即队列完全清空，这也是SPFA的精髓，一旦有点改动，就放入队列，再进行一遍边松弛，如果一直到队列清空，都没有点改动，说明此时已达到最短
         d[]=;
         bool flag=true;
         for (k=;k<=n;k++)
         {
             if (d[k]==inf) {flag=false;break;}
             d[]+=d[k]*vn[k]; //第一个点的点权值无需考虑，对求出的最短路和点值进行相乘累加即是最终答案
         }
         if (!flag) puts("No Answer");
         else
         printf("%lld\n",d[]);
     }
     return ;
}