#Week7 Neural Networks : Learning

一、Cost Function and Backpropagation

神经网络的损失函数：

\[J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2
\]

这个cost function是在logistic regression基础上演变而来，只是神经网络有很多输出结点，而logistic regression只有一个输出结点，所以这个cost function只是把所有的K个输出结点的损失函数进行累加。

得到cost function后，为了寻找使得\(J(\theta)\)最小的那组参数\(\theta\)，我们需要知道\(J(\theta)\)关于每个\(\theta\)的偏导数，而后向传播算法可以帮助我们计算偏导数：



对于每个训练样本，先利用forward propagation计算每一层的\(a\)：



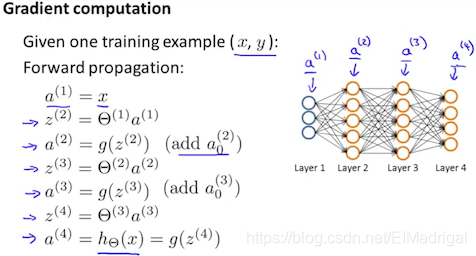
接着利用样本真实标签\(y^{(t)}\)计算最后一层的误差值；

之后从右向左计算每一层（输入层除外）的误差：



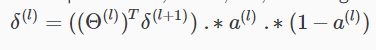
这样每个样本一次正向、一次反向来更新误差矩阵：



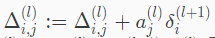
向量化表示：



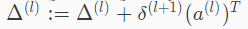
最后，就可以得到偏导数：

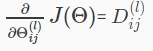
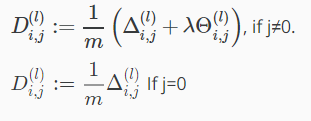
二、Backpropagation in Pratice

为了使用fminunc等高级的优化方法来求得cost function的最小值，所以将\(\theta\)这个矩阵展成向量传入fminunc，完成后可以通过reshape从向量中提取\(\theta^{(1)}、\theta^{(2)}\)等：

为了确保我们使用Backpropagation求得的偏导数的正确性，可以使用Gradient Checking（很慢）来检验：

根据偏导数定义：

\[\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) - J(\Theta_1, \dots, \Theta_j - \epsilon, \dots, \Theta_n)}{2\epsilon}
\]

\[一般\epsilon=10^{-4}
\]

通过将这种方式计算的偏导数与之前Backpropagation求得的偏导数比较，即可得知Backpropagation的正确性。

之前在Linear Regression和Logistic Regression，我们可以用全0来初始化\(\theta\)，但在神经网络中，这样做会有问题，所以采用随机初始化：



最后，从整体捋一遍流程：

1、选择网络结构：



2、训练神经网络：

对每一个训练样本：