【刷题】洛谷 P4716 【模板】最小树形图

题目背景

这是一道模板题。

题目描述

给定包含 \(n\) 个结点， \(m\) 条有向边的一个图。试求一棵以结点 \(r\) 为根的最小树形图，并输出最小树形图每条边的权值之和，如果没有以 \(r\) 为根的最小树形图，输出 \(-1\) 。

输入输出格式

输入格式：

第一行包含三个整数 \(n,m,r\) ，意义同题目所述。

接下来 \(m\) 行，每行包含三个整数 \(u,v,w\) ，表示图中存在一条从 \(u\) 指向 \(v\) 的权值为 \(w\) 的有向边。

输出格式：

如果原图中存在以 \(r\) 为根的最小树形图，就输出最小树形图每条边的权值之和，否则输出 \(-1\) 。

输入输出样例

输入样例#1：

4 6 1

1 2 3

1 3 1

4 1 2

4 2 2

3 2 1

3 4 1

输出样例#1：

3

输入样例#2：

4 6 3

1 2 3

1 3 1

4 1 2

4 2 2

3 2 1

3 4 1

输出样例#2：

4

输入样例#3：

4 6 2

1 2 3

1 3 1

4 1 2

4 2 2

3 2 1

3 4 1

输出样例#3：

-1

说明

样例 \(1\) 解释

最小树形图中包含第 \(2\) ， \(5\) ， \(6\) 三条边，总权值为 \(1 + 1 + 1 = 3\)

样例 \(2\) 解释

最小树形图中包含第 \(3\) ， \(5\) ， \(6\) 三条边，总权值为 \(2 + 1 + 1 = 3\)

样例 \(3\) 解释

无法构成最小树形图，故输出 \(-1\) 。

数据范围

对于所有数据， \(1 \leq u, v \leq n \leq 100\) ， \(1 \leq m \leq 10^4\) ，\(1 \leq w \leq 10^6\) ​​。

题解

最小树形图模板题，打板子就好了

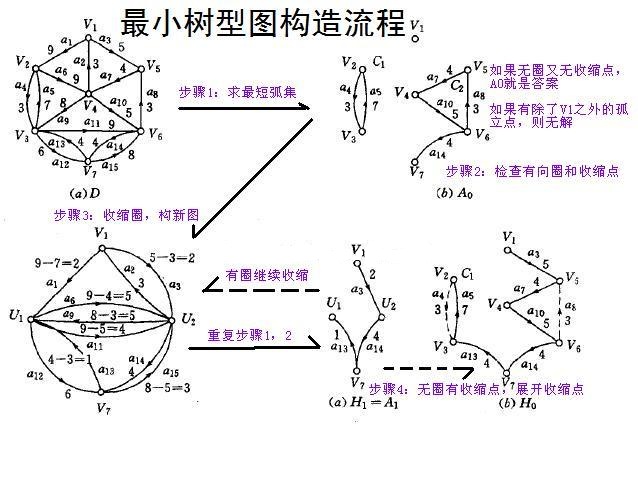
如果你不会最小树形图，看这个图，或者看这里

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=100+10,MAXM=10000+10,inf=0x3f3f3f3f;
int n,m,r,in[MAXN],bel[MAXN],vis[MAXN],pre[MAXN];
struct node{
	int u,v,k;
};
node side[MAXM];
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline int solve(int rt,int n)
{
	int res=0;
	while(true)
	{
		for(register int i=1;i<=n;++i)in[i]=inf;
		for(register int i=1;i<=m;++i)
			if(side[i].u!=side[i].v&&in[side[i].v]>side[i].k)in[side[i].v]=side[i].k,pre[side[i].v]=side[i].u;
		for(register int i=1;i<=n;++i)
			if(i!=rt&&in[i]==inf)return -1;
		int cnt=0;
		memset(bel,0,sizeof(bel));
		memset(vis,0,sizeof(vis));
		in[rt]=0;
		for(register int i=1,j;i<=n;++i)
		{
			res+=in[i];j=i;
			while(j!=rt&&vis[j]!=i&&!bel[j])vis[j]=i,j=pre[j];
			if(j!=rt&&!bel[j])
			{
				bel[j]=++cnt;
				for(register int k=pre[j];k!=j;k=pre[k])bel[k]=cnt;
			}
		}
		if(!cnt)break;
		for(register int i=1;i<=n;++i)
			if(!bel[i])bel[i]=++cnt;
		for(register int i=1,u,v;i<=m;++i)
		{
			u=side[i].u,v=side[i].v;
			side[i].u=bel[u],side[i].v=bel[v];
			if(bel[u]^bel[v])side[i].k-=in[v];
		}
		n=cnt;
		rt=bel[rt];
	}
	return res;
}
int main()
{
	read(n);read(m);read(r);
	for(register int i=1;i<=m;++i)
	{
		int u,v,k;read(u);read(v);read(k);
		side[i]=(node){u,v,k};
	}
	write(solve(r,n),'\n');
	return 0;
}