[Opencv]图像的梯度与边缘检测（转）

文章来源：https://blog.csdn.net/on2way/article/details/46851451

• 梯度简单来说就是求导，在图像上表现出来的就是提取图像的边缘（不管是横向的、纵向的、斜方向的等等），所需要的无非也是一个核模板，模板的不同结果也不同。所以可以看到，所有的这些个算子函数，归结到底都可以用函数cv2.filter2D()来表示，不同的方法给予不同的核模板，然后演化为不同的算子而已。并且这只是这类滤波函数的一个用途，曾经写过一个关于matlab下滤波函数imfilter（）的扩展应用（等同于opencv的cv2.filter2D函数）：

  图像滤波函数imfilter函数的应用及其扩展

  就是很多复杂的计算都是可以通过这个滤波函数组合实现，这样的话速度快。

（一）关于Sobel算子与Scharr算子

Sobel算子是高斯平滑与微分操作的结合体，所以其抗噪能力很强，用途较多。一般的sobel算子包括x与y两个方向，算子模板为：

sobelx=[−101−202−101]" role="presentation">sobelx=⎡⎣⎢−1−2−1000121⎤⎦⎥sobelx=[−101−202−101]

sobely=[−1−2−1000121]" role="presentation">sobely=⎡⎣⎢−101−202−101⎤⎦⎥sobely=[−1−2−1000121]

在opencv函数中，还可以设置卷积核(ksize)的大小，如果ksize=-1,就演变为3*3的Scharr算子，模板无非变了个数字：

scharrx=[−303−10010−303]" role="presentation">scharrx=⎡⎣⎢−3−10−30003103⎤⎦⎥scharrx=[−303−10010−303]

scharry=[−3−10−30003103]" role="presentation">scharry=⎡⎣⎢−303−10010−303⎤⎦⎥scharry=[−3−10−30003103]

贴一个相关详细参考：

OpenCV-Python教程（6、Sobel算子）

(二)关于拉普拉斯(Laplacian)算子

拉普拉斯算子可以实现图像的二阶倒数的定义，至于二阶倒数有什么意义，可以看这位博主的详细介绍：

OpenCV-Python教程（7、Laplacian算子）

其核模板为：

kernel=[0101−41010]" role="presentation">kernel=⎡⎣⎢0101−41010⎤⎦⎥kernel=[0101−41010]

下面是对上述三种模板的实例：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('flower.jpg',0)
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)#默认ksize=3
sobely = cv2.Sobel(img,cv2.CV_64F,0,1)
sobelxy = cv2.Sobel(img,cv2.CV_64F,1,1)
laplacian = cv2.Laplacian(img,cv2.CV_64F)#默认ksize=3
#人工生成一个高斯核，去和函数生成的比较
kernel = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]],np.float32)#
img1 = np.float64(img)#转化为浮点型的
img_filter = cv2.filter2D(img1,-1,kernel)
sobelxy1 = cv2.Sobel(img1,-1,1,1)

plt.subplot(221),plt.imshow(sobelx,'gray')
plt.subplot(222),plt.imshow(sobely,'gray')
plt.subplot(223),plt.imshow(sobelxy,'gray')
plt.subplot(224),plt.imshow(laplacian,'gray')

plt.figure()
plt.imshow(img_filter,'gray')

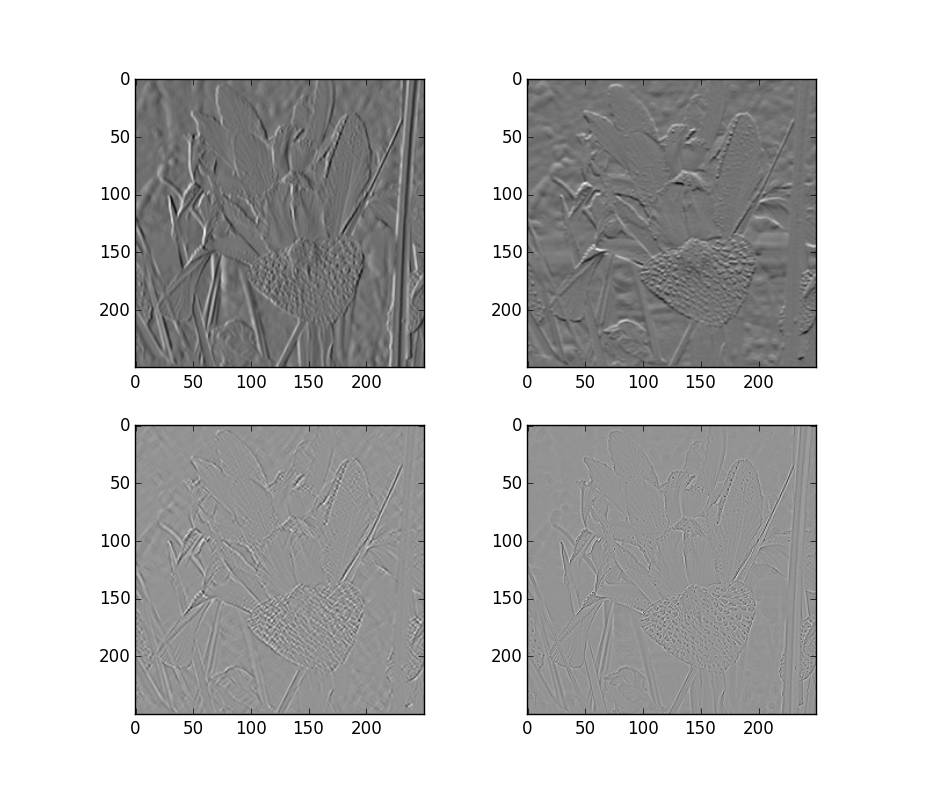
上述一个很重要的问题需要明白的就是，在滤波函数第二个参数，当我们使用-1表示输出图像与输入图像的数据类型一致时，如果原始图像是uint8型的，那么在经过算子计算以后，得到的图像可能会有负值，如果与原图像数据类型一致，那么负值就会被截断变成0或者255，使得结果错误，那么针对这种问题有两种方式改变（上述程序中都有）：一种就是改变输出图像的数据类型（第二个参数cv2.CV_64F），另一种就是改变原始图像的数据类型（此时第二个参数可以为-1，与原始图像一致）。

上述程序从结果上也说明使用函数cv2.filter2D也能达到相同的效果。

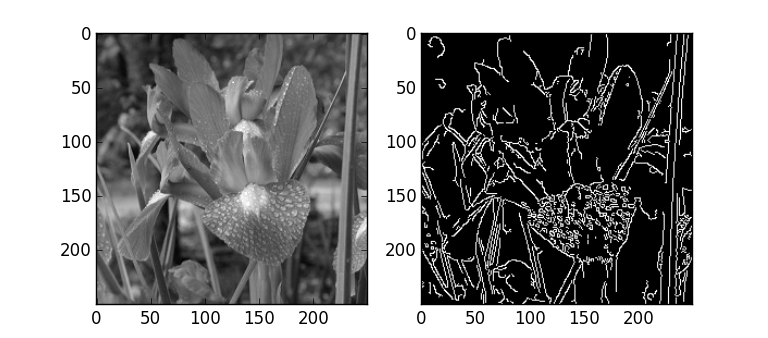
（三）Canny边缘检测算子

关于canny边缘检测算子，细究的话还算比较的复杂，给出一个介绍比较详细的博客吧：

canny算子

那么opencv中的函数也非常简单，直接cv2.Canny()，这个函数需要五个参数，原始图像，两个范围控制值minVal和maxVal（见上述原理介绍）,第四个参数用于规定核模板的大小（默认3），最后一个是true与false（默认）的选择，有一点不同，不太重要，可以试着那个好用那个。

import cv2
import matplotlib.pyplot as plt

img = cv2.imread('flower.jpg',0)
edges = cv2.Canny(img,100,200)#其他的默认
plt.subplot(121),plt.imshow(img,'gray')
plt.subplot(122),plt.imshow(edges,'gray')