对于约束优化问题：

拉格朗日公式：

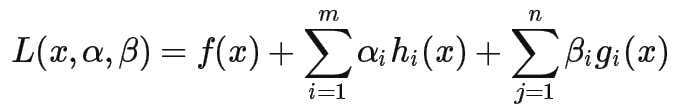
其KKT条件为：

求解 x、α、β

其中β*g(x)为互补松弛条件

KKT条件是使一组解成为最优解的必要条件，当原问题是凸问题的时候，KKT条件也是充分条件。

最优化 KKT条件的更多相关文章

  1. 机器学习——支持向量机(SVM)之拉格朗日乘子法，KKT条件以及简化版SMO算法分析

    SVM有很多实现,现在只关注其中最流行的一种实现,即序列最小优化(Sequential Minimal Optimization,SMO)算法,然后介绍如何使用一种核函数(kernel)的方式将SVM ...

  2. 【整理】深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有不等约束时使用 ...

  3. 深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

    [整理]   在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法.在有等式约束时使用拉格朗日乘子法,在有 ...

  4. 装载：关于拉格朗日乘子法与KKT条件

    作者:@wzyer 拉格朗日乘子法无疑是最优化理论中最重要的一个方法.但是现在网上并没有很好的完整介绍整个方法的文章.我这里尝试详细介绍一下这方面的有关问题,插入自己的一些理解,希望能够对大家有帮助. ...

  5. 寻找“最好”（4）——不等约束和KKT条件

    不等约束 上篇文章介绍了如何在等式约束下使用拉格朗日乘子法,然而真实的世界哪有那么多等式约束?我们碰到的大多数问题都是不等约束.对于不等约束的优化问题,可以这样描述: 其中f(x)是目标函数,g(x) ...

  6. 关于拉格朗日乘子法与KKT条件

    关于拉格朗日乘子法与KKT条件 关于拉格朗日乘子法与KKT条件   目录 拉格朗日乘子法的数学基础 共轭函数 拉格朗日函数 拉格朗日对偶函数 目标函数最优值的下界 拉格朗日对偶函数与共轭函数的联系 拉 ...

  7. KKT条件和拉格朗日乘子法详解

    \(\frac{以梦为马}{晨凫追风}\) 最优化问题的最优性条件,最优化问题的解的必要条件和充分条件 无约束问题的解的必要条件 \(f(x)\)在\(x\)处的梯度向量是0 有约束问题的最优性条件 ...

  8. ML-对偶(Duality)问题 KKT 条件

    Primal => Dual 现实中我们遇到的原优化问题, 写为标准型的话是这样的. \(min _w f(w) \\ s.t. \\ g_i(w) <=0 \\ h_i(w) = 0\) ...

  9. 机器学习——最优化问题：拉格朗日乘子法、KKT条件以及对偶问题

    1 前言 拉格朗日乘子法(Lagrange Multiplier)  和 KKT(Karush-Kuhn-Tucker)  条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等 ...

随机推荐

  1. JavaScript数据结构-7.链表

    <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...

  2. PHP之string之wordwrap()函数使用

    wordwrap (PHP 4 >= 4.0.2, PHP 5, PHP 7) wordwrap - Wraps a string to a given number of characters ...

  3. Win10上使用Linux Subsystem配置cuckoo sandbox

    原文连接:https://www.trustwave.com/Resources/SpiderLabs-Blog/Cuckoo--Linux-Subsystem--Some-Love-for-Wind ...

  4. SharePoint 2007 form.js兼容性修改

    因SharePoint 2007发布时微软的主要IE的版本是7,所以其中不少的JS是不规范的,在新的IE8 9 10 11等版本中碰到不少的问题,以下是部分的修复,记录下,不断完善. ()语法问题 d ...

  5. free 和 delete 把指针怎么了

    使用free或delete之后,只是把指针所指的内容给释放掉,但是指针并没有被干掉,还是指向原来位置(并不是执行NULL),此时指针指向的内容为垃圾,被称为“野指针”. 举例说明几个重要容易迷糊的特征 ...

  6. ios 点击失效、闪屏问题解决方案

    一.点击失效 描述:将点击事件(click)委派在document或者body上,且目标元素为默认不可点击的元素时(非<a>. <button>而是<span>等) ...

  7. CSS3 图标神器 => content:"我是特殊符号"

    基本形状 ▲ 9650 25B2 ► 9658 25BA ► 9658 25BA ▼ 9660 25BC ◄ 9668 25C4 ❤ 10084 2764 ✈ 9992 2708 ★ 9733 260 ...

  8. vuex源码分析3.0.1(原创)

    前言 chapter1 store构造函数 1.constructor 2.get state和set state 3.commit 4.dispatch 5.subscribe和subscribeA ...

  9. Redis常用命令整理

    doc 环境下使用命令:       keys 命令         ?    匹配一个字符         *    匹配任意个(包括0个)字符         []    匹配括号间的任一个字符, ...

  10. golang操作mysql数据库

    golang操作mysql数据库 代码: mysql的增.删.改.查 package main import ( "database/sql" "fmt" &q ...