【BZOJ1101】Zap [莫比乌斯反演]

Zap

Time Limit: 10 Sec  Memory Limit: 162 MB
[Submit][Status][Discuss]

Description

　　对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a，y<=b，并且gcd(x,y)=d。

Input

　　第一行包含一个正整数n，表示一共有n组询问。接下来n行，每行表示一个询问，每行三个正整数，分别为a,b,d。

Output

　　输出一个正整数，表示满足条件的整数对数。

Sample Input

　　2
　　4 5 2
　　6 4 3

Sample Output

　　3
　　2

HINT

　　1<=n<= 50000, 1<=d<=a,b<=50000

Solution

　　我们运用莫比乌斯反演，然后推一下式子得到：

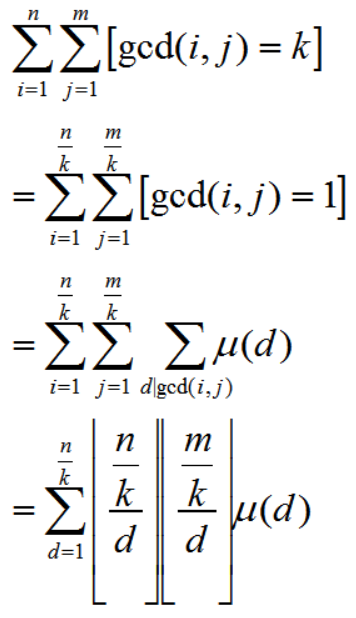
　　我们依旧对于下界分块求解即可。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int ONE = ;

 int T;
 int n,m,k;
 bool isp[ONE];
 int prime[ONE],p_num;
 int miu[ONE],sum_miu[ONE];
 s64 Ans;

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Getmiu(int MaxN)
 {
         miu[] = ;
         for(int i=; i<=MaxN; i++)
         {
             if(!isp[i])
                 prime[++p_num] = i, miu[i] = -;
             for(int j=; j<=p_num, i*prime[j]<=MaxN; j++)
             {
                 isp[i * prime[j]] = ;
                 if(i%prime[j] == )
                 {
                     miu[i * prime[j]] = ;
                     break;
                 }
                 miu[i * prime[j]] = -miu[i];
             }
             miu[i] += miu[i-];
         }
 }

 void Solve()
 {
         n=get();    m=get();    k=get();
         if(n > m) swap(n,m);

         int N = n/k, M = m/k;   Ans = ;
         for(int i=,j=; i<=N; i=j+)
         {
             j = min(N/(N/i), M/(M/i));
             Ans += (s64)(N/i) * (M/i) * (miu[j] - miu[i-]);
         }

         printf("%lld\n",Ans);
 }

 int main()
 {
         Getmiu(ONE-);
         T=get();
         while(T--)
             Solve();
 }