Stack的三种含义 ----超级经典 明白了 栈 的三种含义

来自：http://www.ruanyifeng.com/blog/2013/11/stack.html

------------------------------------------------------------------------

学习编程的时候，经常会看到stack这个词，它的中文名字叫做"栈"。

理解这个概念，对于理解程序的运行至关重要。容易混淆的是，这个词其实有三种含义，适用于不同的场合，必须加以区分。

含义一：数据结构

stack的第一种含义是一组数据的存放方式，特点为LIFO，即后进先出（Last in, first out）。

在这种数据结构中，数据像积木那样一层层堆起来，后面加入的数据就放在最上层。使用的时候，最上层的数据第一个被用掉，这就叫做"后进先出"。

与这种结构配套的，是一些特定的方法，主要为下面这些。

• push：在最顶层加入数据。
• pop：返回并移除最顶层的数据。
• top：返回最顶层数据的值，但不移除它。
• isempty：返回一个布尔值，表示当前stack是否为空栈。

含义二：代码运行方式

stack的第二种含义是"调用栈"（call stack），表示函数或子例程像堆积木一样存放，以实现层层调用。

下面以一段Java代码为例（来源）。

class Student{
    int age;
    String name;      
 
    public Student(int Age, String Name)
    {
        this.age = Age;
        setName(Name);
    }
    public void setName(String Name)
    {
        this.name = Name;
    }
}
 
public class Main{
    public static void main(String[] args) {
            Student s;
            s = new Student(23,"Jonh");
    }
}

上面这段代码运行的时候，首先调用main方法，里面需要生成一个Student的实例，于是又调用Student构造函数。在构造函数中，又调用到setName方法。

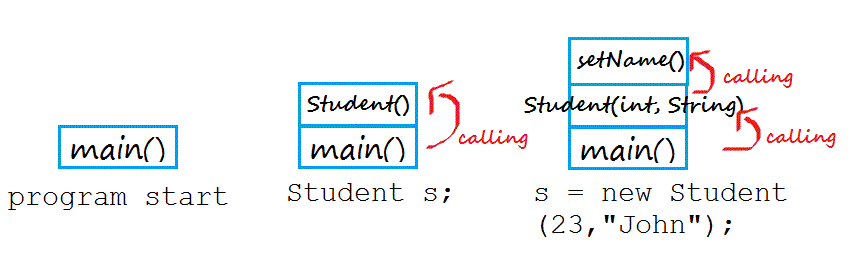
这三次调用像积木一样堆起来，就叫做"调用栈"。程序运行的时候，总是先完成最上层的调用，然后将它的值返回到下一层调用，直至完成整个调用栈，返回最后的结果。

含义三：内存区域

stack的第三种含义是存放数据的一种内存区域。程序运行的时候，需要内存空间存放数据。一般来说，系统会划分出两种不同的内存空间：一种叫做stack（栈），另一种叫做heap（堆）。

它们的主要区别是：stack是有结构的，每个区块按照一定次序存放，可以明确知道每个区块的大小；heap是没有结构的，数据可以任意存放。因此，stack的寻址速度要快于heap。

其他的区别还有，一般来说，每个线程分配一个stack，每个进程分配一个heap，也就是说，stack是线程独占的，heap是线程共用的。此外，stack创建的时候，大小是确定的，数据超过这个大小，就发生stack overflow错误，而heap的大小是不确定的，需要的话可以不断增加。

根据上面这些区别，数据存放的规则是：只要是局部的、占用空间确定的数据，一般都存放在stack里面，否则就放在heap里面。请看下面这段代码（来源）。

public void Method1()
{
    int i=4;
 
    int y=2;
 
    class1 cls1 = new class1();
}

上面代码的Method1方法，共包含了三个变量：i, y 和 cls1。其中，i和y的值是整数，内存占用空间是确定的，而且是局部变量，只用在Method1区块之内，不会用于区块之外。cls1也是局部变量，但是类型为指针变量，指向一个对象的实例。指针变量占用的大小是确定的，但是对象实例以目前的信息无法确知所占用的内存空间大小。

这三个变量和一个对象实例在内存中的存放方式如下。

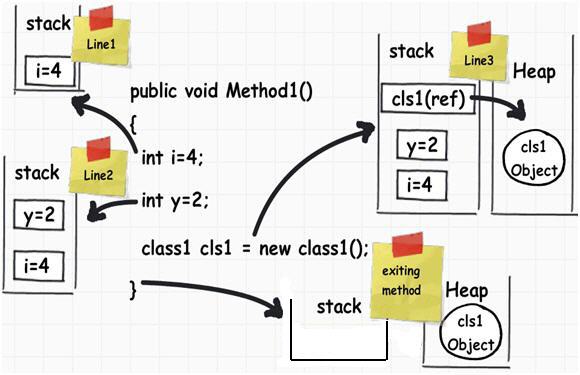
从上图可以看到，i、y和cls1都存放在stack，因为它们占用内存空间都是确定的，而且本身也属于局部变量。但是，cls1指向的对象实例存放在heap，因为它的大小不确定。作为一条规则可以记住，所有的对象都存放在heap。

接下来的问题是，当Method1方法运行结束，会发生什么事？

回答是整个stack被清空，i、y和cls1这三个变量消失，因为它们是局部变量，区块一旦运行结束，就没必要再存在了。而heap之中的那个对象实例继续存在，直到系统的垃圾清理机制（garbage collector）将这块内存回收。因此，一般来说，内存泄漏都发生在heap，即某些内存空间不再被使用了，却因为种种原因，没有被系统回收。

（完）