【题解】洛谷P2822 [NOIP2016TG ]组合数问题 （二维前缀和+组合数）

洛谷P2822：https://www.luogu.org/problemnew/show/P2822

思路

由于n和m都多达2000

所以暴力肯定是会WA的

因为整个组合数是不会变的

所以我们想到存下这个组合数（杨辉三角）阵型

注意要用二维前缀和存下 后来的k次询问就可以用O(1)解答

关于二维前缀和

用此图可以解答：

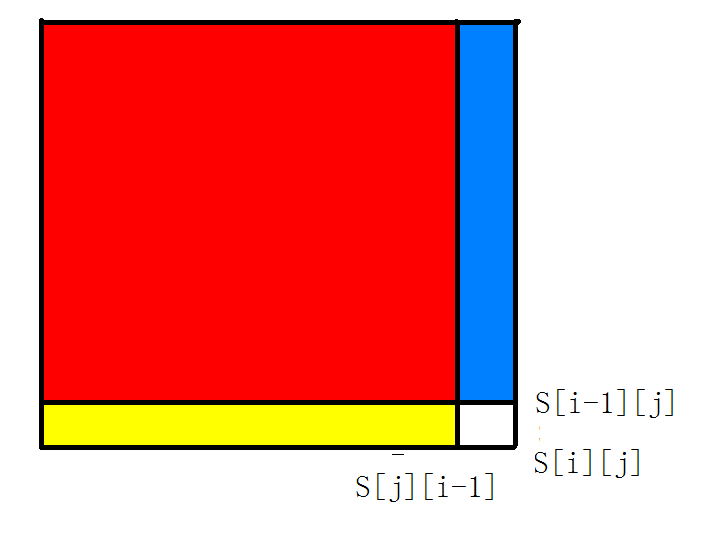
关键代码：s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1];

来自dalao的口诀：上加左 减左上 加自己

代码

#include<iostream>
using namespace std;
#define maxn 2005
int c[maxn][maxn],s[maxn][maxn];
int t,k,m,n;
void build()
{
    for(int i=;i<=;i++)
    {
        c[i][]=c[i][i]=;
        for(int j=;j<=i-;j++)
        c[i][j]=(c[i-][j-]+c[i-][j])%k;//杨辉三角递推
    }
    for(int i=;i<=;i++)
    {
        for(int j=;j<=i;j++)
        {
            s[i][j]=s[i][j-]+s[i-][j]-s[i-][j-];
            if(!c[i][j])//如果c[i][j]为0说明 它是k的倍数
            s[i][j]+=;//ans加1
        }
        s[i][i+]=s[i][i];//详见后文注释<1>
    }
}
int main()
{
    cin>>t>>k;
    build();
    while(t)
    {
        t--;
        cin>>n>>m;
        if(m>n) m=n;//m不能大于n
        cout<<s[n][m]<<endl;
    }
}

注释<1>：

补齐杨辉三角的右上角一排 否则二维前缀和在最右边无法算出

对于k=2

例： 1             0 0             如果不加这句代码    0

1 1          0 0 0                                     0 0

1 2 1       0 1 1 1                                   0 1 0

1 3 3 1    0 1 1 1 1                                 0 1 0 0

对于最右边的一排1的位置的前缀和无法计算 因为没有上面的值