[BZOJ4817]树点涂色

第一个操作比较麻烦，但可以看出它和lct里的access操作差不多，所以可以利用lct的性质巧妙维护操作1

直接用lct维护树中同颜色的链（因为染色操作是从$x$染到根所以同颜色的点一定形成一条链），权值就存$x$到根的路径权值$v_x$

对于操作1，在access每一次切换$x$的实儿子时，把原实儿子在splay中最左的点（也就是在原树中在$x$以下且同一条链上深度最浅的点）的子树权值$+1$，把新实儿子在splay中最左的点的子树权值$-1$（每一次切换，原实儿子的子树到根的路径上多了一种颜色，新实儿子的子树到根的路径上少了一种颜色）

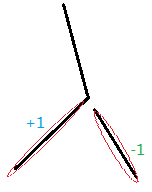
对于操作2，容易看出答案是$v_x+v_y-2v_{lca_{x,y}}+1$

对于操作3，直接用线段树维护dfs序，就是查询区间最大值

这个lct的性质用得好哇

#include<stdio.h>
void swap(int&a,int&b){a^=b^=a^=b;}
int max(int a,int b){return a>b?a:b;}
int n,a[100010];
struct seg{
	int mx[400010],d[400010];
	void pushup(int x){mx[x]=max(mx[x<<1],mx[x<<1|1]);}
	void build(int l,int r,int x){
		if(l==r){
			mx[x]=a[l];
			return;
		}
		int mid=(l+r)>>1;
		build(l,mid,x<<1);
		build(mid+1,r,x<<1|1);
		pushup(x);
	}
	void add(int x,int v){
		d[x]+=v;
		mx[x]+=v;
	}
	void pushdown(int x){
		if(d[x]){
			add(x<<1,d[x]);
			add(x<<1|1,d[x]);
			d[x]=0;
		}
	}
	void modify(int L,int R,int v,int l,int r,int x){
		if(L<=l&&r<=R)return add(x,v);
		pushdown(x);
		int mid=(l+r)>>1;
		if(L<=mid)modify(L,R,v,l,mid,x<<1);
		if(mid<R)modify(L,R,v,mid+1,r,x<<1|1);
		pushup(x);
	}
	int query(int L,int R,int l,int r,int x){
		if(L<=l&&r<=R)return mx[x];
		pushdown(x);
		int mid=(l+r)>>1,ans=-1;
		if(L<=mid)ans=max(ans,query(L,R,l,mid,x<<1));
		if(mid<R)ans=max(ans,query(L,R,mid+1,r,x<<1|1));
		return ans;
	}
}s;
struct tree{
	int h[100010],nex[200010],to[200010],in[100010],ou[100010],fa[100010][17],dep[100010],M;
	void add(int a,int b){
		M++;
		to[M]=b;
		nex[M]=h[a];
		h[a]=M;
	}
	void dfs(int x){
		in[x]=++M;
		for(int i=h[x];i;i=nex[i]){
			if(to[i]!=fa[x][0]){
				fa[to[i]][0]=x;
				dep[to[i]]=dep[x]+1;
				dfs(to[i]);
			}
		}
		ou[x]=M;
	}
	void pre(){
		int i,j,x,y;
		for(i=1;i<n;i++){
			scanf("%d%d",&x,&y);
			add(x,y);
			add(y,x);
		}
		dep[1]=1;
		M=0;
		dfs(1);
		for(j=1;j<17;j++){
			for(i=1;i<=n;i++)fa[i][j]=fa[fa[i][j-1]][j-1];
		}
		for(i=1;i<=n;i++)a[in[i]]=dep[i];
		s.build(1,n,1);
	}
	void modify(int x,int v){
		s.modify(in[x],ou[x],v,1,n,1);
	}
	int get(int x){
		return s.query(in[x],in[x],1,n,1);
	}
	int sub(int x){
		return s.query(in[x],ou[x],1,n,1);
	}
	int lca(int x,int y){
		int i;
		if(dep[x]<dep[y])swap(x,y);
		for(i=16;i>=0;i--){
			if(dep[fa[x][i]]>=dep[y])x=fa[x][i];
		}
		if(x==y)return x;
		for(i=16;i>=0;i--){
			if(fa[x][i]!=fa[y][i]){
				x=fa[x][i];
				y=fa[y][i];
			}
		}
		return fa[x][0];
	}
}t;
struct lct{
	int fa[100010],ch[100010][2],l[100010];
	void pre(){
		int i;
		for(i=2;i<=n;i++)fa[i]=t.fa[i][0];
		for(i=1;i<=n;i++)l[i]=i;
	}
	#define ls ch[x][0]
	#define rs ch[x][1]
	void pushup(int x){
		if(ls)
			l[x]=l[ls];
		else
			l[x]=x;
	}
	void rot(int x){
		int y,z,f,b;
		y=fa[x];
		z=fa[y];
		f=ch[y][0]==x;
		b=ch[x][f];
		fa[x]=z;
		fa[y]=x;
		if(b)fa[b]=y;
		ch[x][f]=y;
		ch[y][f^1]=b;
		if(ch[z][0]==y)ch[z][0]=x;
		if(ch[z][1]==y)ch[z][1]=x;
		pushup(y);
		pushup(x);
	}
	bool isrt(int x){return ch[fa[x]][0]!=x&&ch[fa[x]][1]!=x;}
	void splay(int x){
		int y,z;
		while(!isrt(x)){
			y=fa[x];
			z=fa[y];
			if(!isrt(y))rot((ch[z][0]==y&&ch[y][0]==x)||(ch[z][1]==y&&ch[y][1]==x)?y:x);
			rot(x);
		}
	}
	void access(int x){
		int y=0;
		while(x){
			splay(x);
			if(rs)t.modify(l[rs],1);
			rs=y;
			if(y)t.modify(l[y],-1);
			pushup(x);
			y=x;
			x=fa[x];
		}
	}
}l;
int main(){
	int m,i,x,y;
	scanf("%d%d",&n,&m);
	t.pre();
	l.pre();
	while(m--){
		scanf("%d%d",&i,&x);
		if(i==1)l.access(x);
		if(i==2){
			scanf("%d",&y);
			printf("%d\n",t.get(x)+t.get(y)-(t.get(t.lca(x,y))<<1)+1);
		}
		if(i==3)printf("%d\n",t.sub(x));
	}
}