对正交频分复用OFDM系统的理解

OFDM系统

正交频分复用OFDM（Orthogonal Frenquency Division Multiplexing）是一种多载波调制技术。

基本思想：在发送端，它将高速串行数据经过串并变换形成多路低速数据分别对多个正交的子载波进行调制，迭加后构成发送信号。在接收端，用同样数量的载波进行相干解调，获得低速率数据流，经过并串变换形成高速数据流。

主要优点：提高频带利用率，有效抑制符号间干扰(Inter Symbol Interference，ISI)，有很好的抗多径延迟和衰落的性能。

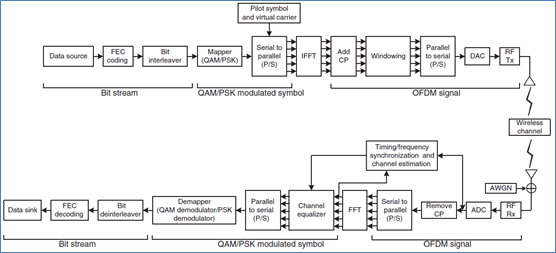
图一 OFDM系统框图

OFDM也是一种FDM频分复用系统。在传统的频分方法中，将频带划分为若干个不相交的子频带来传输并行的数据流，在接收端用一组滤波器来分离各个子信道，子信道之间要留有保护频带，因此这种方法的频带利用率低。OFDM由大量在频率上等间隔的子载波构成，这些子载波的频谱可以相互重叠，这样，大大提高了频谱利用率。并且子载波在整个符号周期上是相互正交的，即加于符号周期上的任何两个子载波的乘积积分等于零。这样，即使各子载波频谱间存在重叠，也能无失真地复原。

当载波间的最小间隔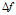等于符号周期T的倒数的整数倍时，可满足正交条件。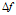不能设计过小，过小的话，对抗多普勒频移的影响能力下降，无法支撑高速移动的无线通信, 不能设计过大，过大的话，OFDM符号周期T就会过小，于是为克服子载波间的干扰，加入CP的开销相对于有用符号来说就会过大，使传送效率受到影响。为实现最大频谱效率，一般取载波最小间隔为符号周期的倒数，。比如在LTE物理层，子载波的间隔Δf=15kHz，一个OFDM symbol的发送时间是66.7us。

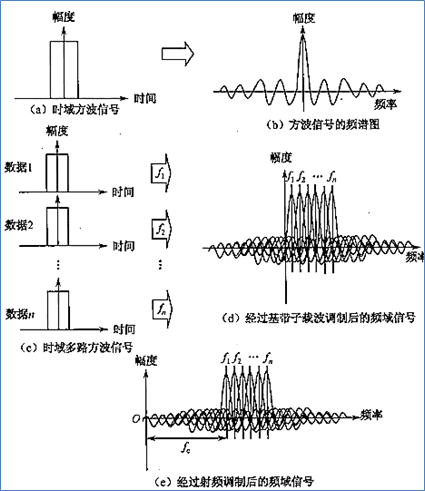
图二 OFDM调制后的信号频谱

如图二所示，时域的方波在频域对应sinc()函数，时域的正余弦信号在频域对应一个单频的冲击信号，因此时域的方波信号经过正交子载波调制后，在频域对应sinc()函数的不同搬移（时域的乘积对应频域的卷积），叠加后的效果如图二(d)，再经过的调制，频谱如图二(e)所示。可以观察出，与传统FDM不同，经过OFDM调制后的信号频谱是交叠的，因此有效提高了频带利用率。

使用IDFT-DFT来实现OFDM

设OFDM信号发射周期为[0，T]，在一个周期内传输N个符号(C₀，C₁，…，C_N-1)，其中C_k为PSK或者QAM调制后的复数，表示相位或者幅度信息。

第k个符号信息调制在第k个载波上，合成的OFDM信号为

图三 OFDM调制解调过程

一般在OFDM系统中，f_k为，f_c为系统的发射载频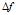，为子载频间的最小间隔，一般取

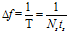
X(t)的低通复包络为：

如果以为采样频率对S(t)采样，[0，T]内共有N_s个样值：

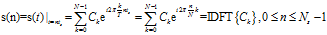
如图四所示，直观上理解，就是每一个OFDM符号信息对应相当于一个单频的频谱，其余采样点的值为0，第i个符号对应的载波频率是i/Nifft或者N-i/Nifft,幅度为d(i)（即上述公式中的C_k），使用IFFT将离散频域变换到连续的时域，对应时域载波,变换后以Nifft个离散点存储，对所有符号的Nifft个离散点求和，即可得到OFDM信号(离散点表示连续信息)。

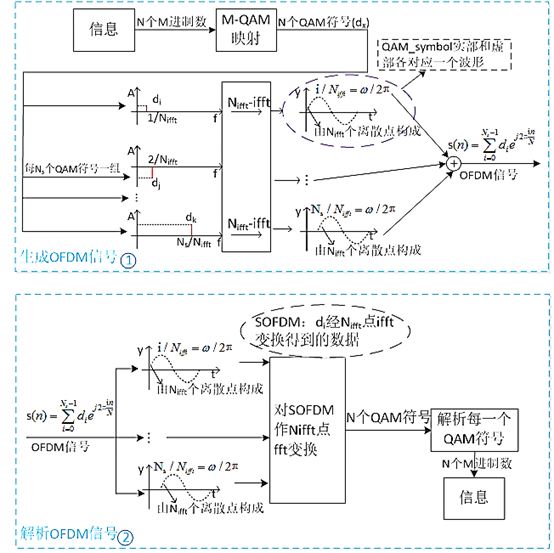
图四 基于IDFT和DFT的示意图

加入循环前缀(Cyclic Prefix，CP)：

由于是多径信道，各路子载波被接收到的时间可能有偏差，这就造成在FFT积分时间长度内子载波之间相差不再是整数周期，子载波之间的正交性受到破坏，如果保护间隔中只是单纯地填零，那么在解调时子载波之间就会产生干扰。循环前缀是将符号尾部的信号复制搬移到前方构成的。当多径时延小于保护间隔时，由于在传输之前已经把尾部的一段信息复制到头部，即使由于时延在接收端损失了一部分信息，但是头部的信息依然可以检测到。这样，就可以保证各路子载波在一次FFT积分时间长度内，各子载波之间相差总是整数个周期，避免了ISI干扰。

图五 循环前缀

---

References:

[1] 正交频分复用_OFDM_及其在高速数字通信中的应用_梅剑平

[2] 正交频分复用_OFDM_技术及其应用_彭宏

[3] LTE学习笔记四：OFDM - CSDN博客

[4] OFDM符号的生成与解析 - CSDN博客

[5] OFDM的发送和接收 —— 按照框图模块化