【LeetCode】最大子阵列 Maximum Subarray（贪婪&分治）

描述：

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

思路一：动态规划

因为这是个优化问题。并且问题可以分解为一个个子问题，所以利用DP来解决此问题是一种很好的解决方案：

dp[i-1]到dp[i]的转换分两种情况：

　　　　　　　　1）dp[i-1] > 0： 当大于0时，dp[i] = dp[i-1] + num[i]

　　　　　　　　2) dp[i-1] < 0：当大于0时，dp[i] = 0  （因为此时将剔除dp[i-1]的影响）

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size());
        dp[] = nums[];
        int max_ans = dp[];
        for(int i = ;i<nums.size();++i){
            dp[i] = nums[i] + (dp[i-] >  ? dp[i-] : );
            max_ans = max(max_ans, dp[i]);
        }
        return max_ans;
    }
};

思路二：贪婪

从左到右汇总数组时找到总和最优解，和dp类似，但是我们这里不保存dp的状态，只记录临时sum和最大sum

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = ;
        int ans;
        ans = nums[];
        for(int i = ;i<nums.size();i++){
            sum+=nums[i];
            ans = max(ans,sum);
            sum = max(sum,);
        }
        return ans;
    }
};

思路三：分治法

分治法的思路是将问题不断二分，分到不能再分，然后再将计算完的数据整合归一，最后得出最优解，这里，如图所示，将数组不断二分，然后取出每一段的最大sum，然后传回总函数，然后输出最优解

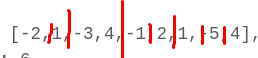
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==) return ;
        return maxSubArray(nums,  , nums.size() - );
    }

    // l代表数组左端low，h代表数组右端high，返回最大sum
    int maxSubArray(vector<int>& arr, int l, int h)
    {
        // Base Case: Only one element
        if (l == h)
            return arr[l];

        // Find middle point
        int m = (l + h)/;

        /* Return maximum of following three possible cases
           a) Maximum subarray sum in left half
           b) Maximum subarray sum in right half
           c) Maximum subarray sum such that the subarray crosses the midpoint */
        return max(max(maxSubArray(arr, l, m),  //最左侧数组求最大sum
                       maxSubArray(arr, m+, h)),  //对右侧数组求最大sum ，之后求左右的最大值
                   maxCrossingSum(arr, l, m, h));  //对整个数组以mid为分界线求最大sum
    }

    int maxCrossingSum(vector<int>& arr, int l, int m, int h)
    {
        // Include elements on left of mid.
        int sum = ;
        int left_sum = INT_MIN;
        for (int i = m; i >= l; i--)
        {
            sum = sum + arr[i];
            if (sum > left_sum)
                left_sum = sum;
        }

        // Include elements on right of mid
        sum = ;
        int right_sum = INT_MIN;
        for (int i = m+; i <= h; i++)
        {
            sum = sum + arr[i];
            if (sum > right_sum)
                right_sum = sum;
        }

        // Return sum of elements on left and right of mid
        return left_sum + right_sum;
    }
};