Codeforces Round #311 (Div. 2) E - Ann and Half-Palindrome（字典树+dp）

E. Ann and Half-Palindrome

time limit per test

1.5 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Tomorrow Ann takes the hardest exam of programming where she should get an excellent mark.

On the last theoretical class the teacher introduced the notion of a half-palindrome.

String t is a half-palindrome, if for all the odd positions i ()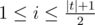
the following condition is held: ti = t|t| - i + 1,
where |t| is the length of string tif
positions are indexed from 1. For example, strings "abaa",
"a", "bb", "abbbaa"
are half-palindromes and strings "ab", "bba"
and "aaabaa" are not.

Ann knows that on the exam she will get string s, consisting only of letters a and b,
and number k. To get an excellent mark she has to find the k-th
in the lexicographical order string among all substrings of s that are half-palyndromes. Note that each substring in this order is
considered as many times as many times it occurs in s.

The teachers guarantees that the given number k doesn't exceed the number of substrings of the given string that are half-palindromes.

Can you cope with this problem?

Input

The first line of the input contains string s (1 ≤ |s| ≤ 5000),
consisting only of characters 'a' and 'b',
where |s| is the length of string s.

The second line contains a positive integer k —  the lexicographical number of the requested string among all the half-palindrome substrings
of the given string s. The strings are numbered starting from one.

It is guaranteed that number k doesn't exceed the number of substrings of the given string that are half-palindromes.

Output

Print a substring of the given string that is the k-th in the lexicographical order of all substrings of the given string that are
half-palindromes.

Sample test(s)

input

abbabaab
7

output

abaa

input

aaaaa
10

output

aaa

input

bbaabb
13

output

bbaabb

Note

By definition, string a = a1a2... an is
lexicographically less than string b = b1b2... bm,
if either a is a prefix of b and
doesn't coincide withb, or there exists such i,
that a1 = b1, a2 = b2, ... ai - 1 = bi - 1, ai < bi.

In the first sample half-palindrome substrings are the following strings — a, a, a, a, aa, aba, abaa, abba, abbabaa, b, b, b, b, baab,bab, bb, bbab, bbabaab (the
list is given in the lexicographical order).

http://codeforces.com/contest/557/problem/E

大致题意：找出s的子串中字典序第k小的“半回文串”，给出半回文串定义是：对于随意i<=|s|/2 有s[i] = s[len-i+1]

数据量是5000

O（n^2）的算法可行

简单暴力的方法就是n^2 dp 出（i,j）的子串是不是半回文串，再把全部子串插入字典树。在dfs遍历出第k小的串

方法二，dp[i][j]统计出以i为始端到i~j的子串是回文串的总数。再把全部子串插入字典树，然后二分出答案子串。

方法一：

#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
using namespace std;
typedef long long ll;

const int N = 5000+5;
int dp[N][N];
char s[N];
int k;
int n;
struct node
{
    node *son[2];
    int cnt;
    node()
    {
        memset(son,0,sizeof(son));
        cnt = 0;
    }
}trie[N*N];
int SZ = 0;
node *root,*cur;
node *createnode()
{
    return &trie[SZ++];
}
void Insert(int p)
{
    cur = root;
    for(int i = p;i <= n;i++)
    {
        int val = s[i]-'a';
        if(cur->son[val] == NULL) cur->son[val] = createnode();
        cur = cur->son[val];
        cur->cnt += dp[p][i];
    }
}
int getsum(node *cur)
{
    int sum = 0;
    if(cur->son[0]) sum += getsum(cur->son[0]);
    if(cur->son[1]) sum += getsum(cur->son[1]);
    cur->cnt += sum;
    return cur->cnt;
}
vector<char>ans;
bool dfs(node *cur,int &k)
{
    if( k <= 0) return true;
    if(cur->son[0])
    {
        ans.push_back('a');
        if(cur->son[0]->cnt) k -= cur->son[0]->cnt;
        if(dfs(cur->son[0],k)) return true;
        ans.pop_back();
    }
    if(cur->son[1])
    {
        ans.push_back('b');
        if(cur->son[1]->cnt)k -= cur->son[1]->cnt;
        if(dfs(cur->son[1],k)) return true;
        ans.pop_back();
    }
    return false;
}
int main()
{
    scanf("%s%d",s+1,&k);
    n = strlen(s+1);
    for(int i =0;i <= n+2;i++)
        for(int j = i;j >= 0;j--)
            dp[i][j] = 1;
    for(int len = 2;len <= n;len++)
        for(int l = 1;l+len-1 <= n;l++)
        {
            int r = l+len-1;
            dp[l][r] = (s[l] == s[r] && dp[l+2][r-2]);
        }
    root = createnode();
    REP(i,n)Insert(i);
    dfs(root,k);
    foreach(i,ans) putchar(*i);
}

方法二：

//GNU C++	Accepted	374 ms	392200 KB
#include <iostream>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <sstream>
#include <string>
#include <vector>
#include <cstdio>
#include <ctime>
#include <bitset>
#include <algorithm>
#define SZ(x) ((int)(x).size())
#define ALL(v) (v).begin(), (v).end()
#define foreach(i, v) for (__typeof((v).begin()) i = (v).begin(); i != (v).end(); ++ i)
#define REP(i,n) for ( int i=1; i<=int(n); i++ )
using namespace std;
typedef long long ll;

const int N = 5000+5;
int dp[N][N];
char s[N];
int k;
int n;
struct node
{
    node *son[2];
    int cnt;
    node()
    {
        memset(son,0,sizeof(son));
        cnt = 0;
    }
}trie[N*N];
int SZ = 0;
node *root,*cur;
node *createnode()
{
    return &trie[SZ++];
}
void Insert(int p)
{
    cur = root;
    for(int i = p;i <= n;i++)
    {
        int val = s[i]-'a';
        if(cur->son[val] == NULL) cur->son[val] = createnode();
        cur = cur->son[val];
        if(i != p)cur->cnt += dp[p][n]-dp[p][i-1];
        else cur->cnt += dp[p][n];
    }
}

void query(node*cur,int k) //二分过程
{
    if(k <= 0) return ;
    if(cur->son[0] && cur->son[0]->cnt >= k)
    {
        int cnt = cur->son[0]->cnt;
        cur = cur->son[0];
        if(cur->son[0]) cnt -= cur->son[0]->cnt;
        if(cur->son[1]) cnt -= cur->son[1]->cnt;
        putchar('a');
        query(cur,k-cnt);
    }
    else if(cur->son[1])
    {
        if(cur->son[0]) k -= cur->son[0]->cnt;
        int cnt = cur->son[1]->cnt;
        cur = cur->son[1];
        if(cur->son[0]) cnt -= cur->son[0]->cnt;
        if(cur->son[1]) cnt -= cur->son[1]->cnt;
        putchar('b');
        query(cur,k-cnt);
    }
}

int main()
{
    scanf("%s%d",s+1,&k);
    n = strlen(s+1);
    for(int i =0;i <= n+2;i++)
        for(int j = i;j >= 0;j--)
            dp[i][j] = 1;
    for(int len = 2;len <= n;len++)
        for(int l = 1;l+len-1 <= n;l++)
        {
            int r = l+len-1;
            dp[l][r] = (s[l] == s[r] && dp[l+2][r-2]);
        }

    REP(i,n)
        for(int j = i+1;j <= n;j++) dp[i][j] += dp[i][j-1];
    root = createnode();
    REP(i,n) Insert(i);
    query(root,k);
}