KMP原理、分析及C语言实现

（是在matrix67博客基础上整理而来，整理着：华科小涛@http://www.cnblogs.com/hust-ghtao/）

有些算法可以让人发疯，KMP算法就是一个。在网上找了很多资料讲的都让人摸不着头脑，本文试图将此算法的思想及实现讲清楚。分为三个部分：基本思想、next[]数组的求法和代码实现。

1 KMP算法基本思想

KMP算法是用来进行字符串匹配的。在上篇文章中我们介绍了字符串匹配的模式匹配法，我们知道若主串的长度为n，m为要匹配的子串的长度，时间复杂度为O(m*n)。在计算机的运算当中，模式匹配的操作随处可见，而模式匹配算法就太低效了。所以就有人提出了KMP算法，它的复杂度只有O(m+n)，之所以叫做KMP算法，是因为这个算法是由Kuuth、Morris、Pratt三个人提出来的，取了他们名字的首字母命名。

为了后续介绍方便，先给出关于字符串的两个概念：“前缀”和“后缀”。“前缀”指除了最后一个字符以外，一个字符串的全部头部组合；“后缀”指除了第一个字符以外，一个字符串的全部尾部组合。如下：

假如母串A=”abababaababacb”,模式串B=”ababacb”，分别以i和j表示其字符的索引，当A[i-j+1…i]与B[1…j]完全相等时，下一次比较A[i+1]和B[j+1]，若想等则i和j各加1；若不相等呢？朴素模式匹配算法是通过i值的回溯来继续进行匹配的；KMP的策略是i不进行回溯，在此基础上调整j的位置（减小j值）使得A[i-j+1…i]与B[1…j]仍然相等，并继续比较A[i+1]和B[j+1]，若想等则i、j各加1，否则重新调整j的值。

这里有两个关键：KMP算法是正确的吗？若是正确的，调整j的原则是什么 ？对于第一个问题请参考《算法导论》。我们来看第二个问题：调整j的原则。原则当然是为目的服务的，我们的目的是进行匹配字符串，即j在大小变化过程当中，能否从最开始的1变化到m，所以为了尽快达到m，调整后的j当然越大越好。就以A、B匹配为例：

（1）当i=j=5时的情况

此时，A[6]≠B[6]，则j不能等于5了，我们要将j减小，减小之后要满足A[5]及其之前的部分仍然匹配。假设j=4可以吗？显然不行A[5]≠B[4] ；j=3呢，满足条件A[5]=B[3] ，于是，i变成了6，而j则变成了 4：

我们发动脑筋仔细想一下，看能不能找到一些规律，对j的值进行调整，也不能挨个试吧！仔细观察上述调整，在j变化之前A[1…5]和B[1…5]完全匹配。调整之后，A[3…5]和

B[1…3]和也完全匹配。也就是说在进行调整时，i保持不变，j变成j',调整后应该满足以A[i]结尾的长度为j'的字符串正好匹配B串的前j各字符，也就是使得A[i-j'+1…i]与B[1…j']仍然相等，调整之前是A[i]结尾的长度为j'的字符串是与B串的后面j'个字符匹配的，调整的过程就是用B串的长度为j'的前缀，代替了B串的长度为j'的后缀的长度，当然为了尽快完成匹配，j'的长度是越大越好。说白了就是当匹配不下去了，就要进行调整，KMP算法要求i的值不能进行回溯，只能调整j值了，当然可以让j从1重新开始，但是之前的匹配就浪费了，能最大限度的避免重复匹配，就找B[1…j]串的前缀和后缀的最长的共有元素，就可以将B串整体后移，用B[1…j]串前缀中的此元素代替后缀中的此元素，由于是同一个串，自然匹配，也就是使得A[i-j'+1…i]与B[1…j']仍然相等。B[1…j']就是此共有元素了，其长度就是j调整后的值。即可以得出结论：当A[i-j+1…i]与B[1…j]完全相等时，下一次比较A[i+1]和B[j+1]，若想等则i和j各加1；若不相等呢KMP的策略是i不进行回溯，在此基础上减小j值，调整为B[1…j]串的前缀和后缀的最长共有元素的长度。

为了加深理解，也为了验证上述结论，我们将这个例子完成j=3时，可以发现B[4]、B[5]分别和A[6]、A[7]相等，i变成7，j变成5，比较A[i+1]和B[j+1]，A[8]和B[6]不相等，仍需调整j：

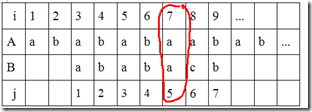
j=5，调整为多少合适呢？根据以上结论，应该调整为B[1…5]串即“ababa”，的前缀和后缀的最长共有元素的长度，根据前缀和后缀的概念，“ababa”的前缀有a、ab、aba、abab，后缀有b、ba、aba、baba，最长共有元素为aba，长度为3，所以j应该减小为3：

看下调整之后的结果，A[i-j+1…i]与B[1…j]仍然相等，即A[5…7]和B[1…3]仍然匹配。在比较A[i+1]和B[j+1]，即A[8]和B[4]仍不等，需要继续减小j。j当前的值为3，所以我们需要求出B[1…3]这个串的前缀和后缀的最长共有元素的长度，显然“aba”的前缀和后缀的最长共有元素的长度为1，所以j减小为1：

调整之后，A[i-j+1…i]与B[1…j]仍然相等，即A[7]和B[1]仍然匹配。在比较A[i+1]和B[j+1]，即A[8]和B[2]仍不等，需要继续减小j。j当前的值为1，所以我们需要求出B[1]这个串的前缀和后缀的最长共有元素的长度，显然“a”的前缀和后缀的最长共有元素的长度为0，所以j减小为0：

再次比较A[i+1]和B[j+1]，终于A[8]=B[1]，可以发现后面的字符串都能直接匹配，所以匹配成功。事实上，有可能j调整到0，仍然不能满足A[i+1]=B[j+1]，那j=0时，我们需要增加i的值，j不变，直到出现，A[i]=B[1]为止。

匹配完了，将算法总结一下吧：当A[i-j+1…i]与B[1…j]完全相等时，下一次比较A[i+1]和B[j+1]，若想等则i和j各加1；若不相等呢KMP的策略是i不进行回溯，在此基础上减小j值，调整为B[1…j]串的前缀和后缀的最长共有元素的长度。 我们发现，新的j值取值为多少与iA串无关，至于B串有关。每次进行这里有一个问题需要解决，就是求出B[1…j]串的前缀和后缀的最长共有元素的长度，从而作为j下次的取值，我们将这个长度的值先计算出来，存放到一个next[]数组当中，在进行匹配时直接读取里面的值就好了。假设我们已经求得

next[]（下标从1始），其中next[j]表示B[1…j]的前缀和后缀的最长共有元素的长度。则KMP算法的伪代码如下：

   1: j=0;

   2: for i=1 to n 

   3: ｛ 

   4:         while (j>0) and (B[j+1]≠A[i]) 

   5:            j=next[j] ;

   6:  

   7:        if B[j+1]==A[i] 

   8:            j=j+1 ;

   9:  

  10:        if j==m then

  11:       ｛

  12:             print('Pattern occurs with shift ',i-m) ;

  13:            j=next[j] ;

  14:        ｝

  15: ｝

  16:  

最后的j=next[j]是为了上程序继续匹配下去，因为有可能找到多出匹配。毋须多言，上述算法和代码已经讲的很清楚了。我们还遗留了一个问题，就是如何求得next[]数组？

2 next[]数组的求法

对于B=“ababacb”我们如何求它的next[]数组呢，大家肯定会想出各种办法，但时间复杂度有好有坏，不用着急！我们的前辈呢，已经帮我们找到了一个比较好的办法，假设B的长度为m，其复杂度只有O（m），但是还是有点难理解的，先将代码写在这里，然后再做分析：

   1: next[1]=0 ;

   2: j=0 ;

   3: for i = 2 to m 

   4: ｛ 

   5:    while (j>0) and (B[j+1]≠B[i]) 

   6:        j = next[j];

   7:    if B[j+1]==B[i] 

   8:      j=j+1;

   9:  

  10:    next[i]=j ;

  11: ｝

整体思路就是：将next[1]的值赋为1，i值从2到m进行循环，可求出next[2…m]，最关键的是while循环里面做的事情。假如已经求得next[1]、next[2]…next[j-1]，我们分析求next[j]的过程，这其实是一个递推的过程，就是B串本身的前缀和后缀之间的匹配过程。就已本例来说明求next[]串的方法：

（1）初始化next[1]=2;

（2）i=2，j=0， while循环条件不成立，if语句：B[1]=a≠B[2]=b，则执行next[i]=j，得到next[2]=0;

（3）i=3，j=0，while循环条件不成立，if语句：B[1]=a=B[3]，则j=j+1，j为1，则执行next[i]=j， 得到next[3]=1;

（4）i=4，j=1，while循环条件不成立，if语句：B[2]=a=B[4]，则j=j+1，j为2，则执行next[i]=j， 得到next[4]=2;

（5）i=5，j=2，while循环条件不成立，if语句：B[3]=a=B[5]，则j=j+1，j为3，则执行next[i]=j， 得到next[5]=3;

（6）i=6，j=3，while循环条件成立：

注意这里进行判断，是判断B[i]和B[j+1]是否相等，即B[j+1]即B[next[i-1]+1]，next[i-1]就是B[1…i-1]的前后缀最大共有元素的长度，这里由于next[5]=3，所以是判断B[5]

和B[3+1]是否相等，由上图看出不相等。如果相等，next[i]=next[i-1]+1，因为B[1…i-1]的长度为next[i-1]的前缀和长度为next[i-1]的后缀是匹配的，若这个前缀的下一个元素B[next[i-1]+1]和这个后缀的下一个元素B[i]相等，说明B[1…i]的前后追最大共有元素的长度为next[i-1]+1。

到这还可以理解，但是B[i]和B[j+1]不相等，即B[6]≠B[4]，我们看上述程序，i=6，j=3，执行的语句是 j=next[j]，即j=1：

我们先看前一个图，由于next[5] =3，所以想让B[1…5]的前后缀的最大共有元素进行匹配，在判断前缀和后缀后面的元素是否匹配，如果匹配的话，next[i]=next[i-1]+1。

如果不想等，也是要调整j的值，调整的思想和KMP主程序的思想一样，都是将j减小到B[1…j]的前后缀的最大共有元素，用前缀代替后缀，继续进行匹配。

3 算法复杂度

KMP算法的复杂度O(m+n)。这个算法分成两部分：主程序和求next[]数组的部分。我们先来分析主程序的复杂度：假设主串的长度为n，主要的争议在于，while循环使得执行次数出现了不确定因素。我们将用到时间复杂度的摊还分析中的主要策略，简单地说就是通过观察某一个变量或函数值的变化来对零散的、杂乱的、不规则的执行次数进行累计。KMP的时间复杂度分析可谓摊还分析的典型。我们从上述程序的j 值入手。每一次执行while循环都会使j减小（但不能减成负的），而另外的改变j值的地方只有第8行。每次执行了这一行，j都只能加1；因此，整个过程中j最多加了n个1。于是，j最多只有n次减小的机会（j值减小的次数当然不能超过n，因为j永远是非负整数）。这告诉我们，while循环总共最多执行了n次。按照摊还分析的说法，平摊到每次for循环中后，一次for循环的复杂度为O(1)。整个过程显然是O(n)的。这样的分析对于后面P数组预处理的过程同样有效，同样可以得到预处理过程的复杂度为O(m)。所以KMP算法的复杂度O(m+n)。