NOIP2009 压轴---最优贸易

链接：https://ac.nowcoder.com/acm/contest/959/H
来源：牛客网

C国有n个大城市和m条道路，每条道路连接这n个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这m条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为1条。
C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到C国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设C国n个城市的标号从1∼n1 \sim n1∼n，阿龙决定从1号城市出发，并最终在n号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有n个城市。
阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品——水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来C国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。
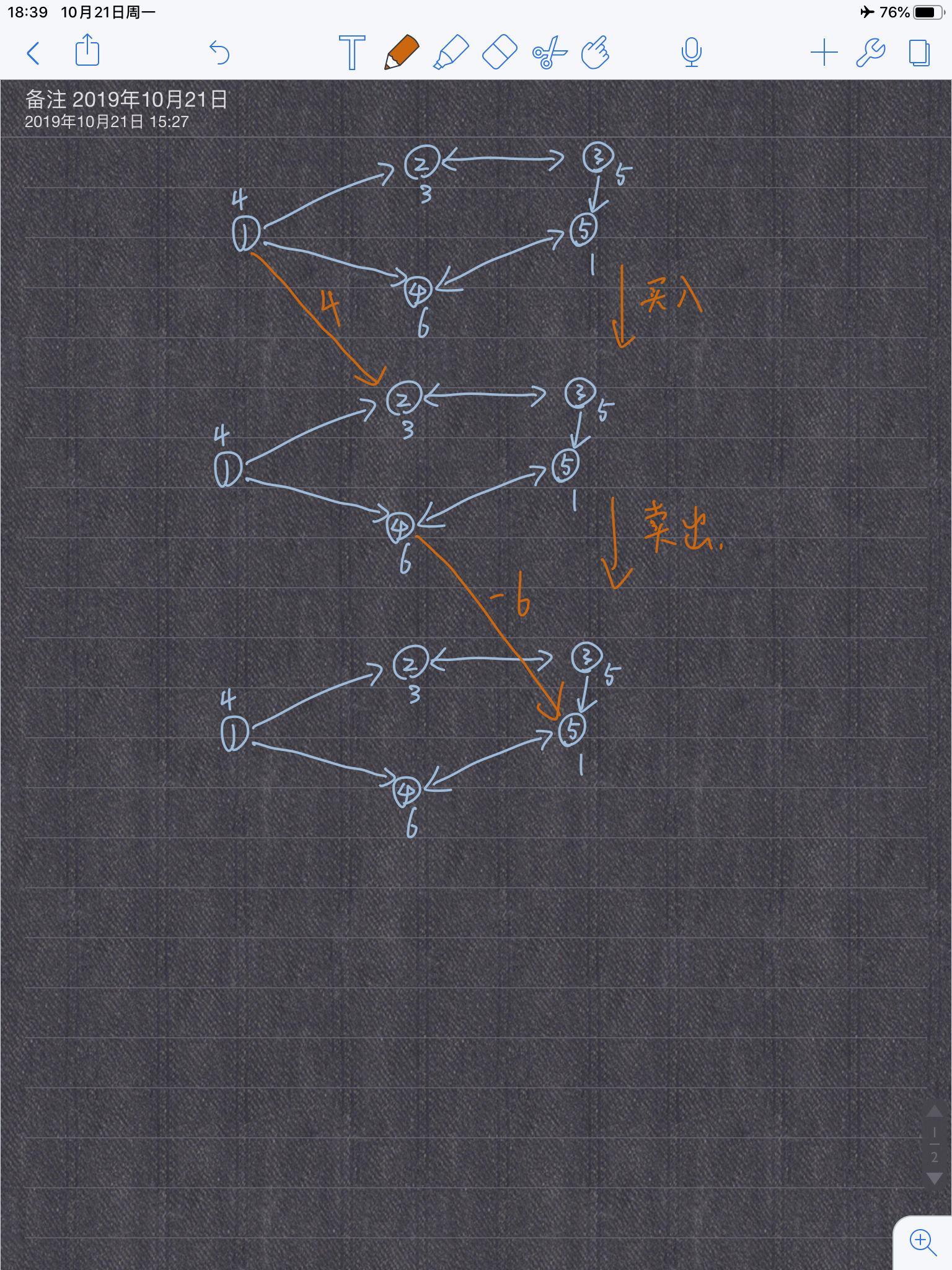
假设C国有5个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

假设1~n号城市的水晶球价格分别为4,3,5,6,1。
阿龙可以选择如下一条线路：1→2→3→51 \to2 \to3 \to51→2→3→5，并在2号城市以3的价格买入水晶球，在3号城市以5的价格卖出水晶球，赚取的旅费数为2。
阿龙也可以选择如下一条线路1→4→5→4→51 \to4 \to5 \to4 \to51→4→5→4→5，并在第1次到达5号城市时以1的价格买入水晶球，在第2次到达4号城市时以6的价格卖出水晶球，赚取的旅费数为5。
现在给出n个城市的水晶球价格，m条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入描述:

输入第一行包含2个正整数n和m，中间用一个空格隔开，分别表示城市的数目和道路的数目。
第二行n个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这n个城市的商品价格。
接下来m行，每行有3个正整数，x,y,z，每两个整数之间用一个空格隔开。如果z=1，表示这条道路是城市x到城市y之间的单向道路；如果z=2，表示这条道路为城市x和城市y之间的双向道路。

输出描述:

输出共1行，包含1个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出0。

链接：https://ac.nowcoder.com/acm/contest/959/H
来源：牛客网

输入

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2

输出

5

题解1：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<vector>
#include<algorithm>
#define maxn 300050
using namespace std;
const int N = 100010;
struct Node {
	int p;
	int len;
	Node(int a, int b) :p(a), len(b) {}
};
int vis[maxn];
int dis[maxn];
int list[maxn];
vector<Node>G[maxn];
void insert(int be, int en) {
	G[be].push_back(Node(en, 0));
	G[be].push_back(Node(en + N, list[be]));

	G[be + N].push_back(Node(en + N, 0));
	G[be + N].push_back(Node(en + N * 2, -list[be]));

	G[be + N + N].push_back(Node(en + N + N, 0));
}
int n, m;

int spfa(int be) {
	memset(dis, 0x3f3f3f3f, sizeof(dis));
	queue<int>que;
	que.push(be);
	dis[be] = 0;
	dis[be + N] = 0;
	dis[be + N + N] = 0;
	while (!que.empty()) {
		int x = que.front();
		que.pop();
		//cout << x << endl;
		vis[x] = 0;
		for (int i = 0; i < G[x].size(); i++) {
			int p = G[x][i].p;
			if (dis[p] > dis[x] + G[x][i].len) {
				dis[p] = dis[x] + G[x][i].len;
				if (!vis[p]) {
					que.push(p);
					vis[p] = 1;
				}
			}
		}
	}
	return 0;
}
int main() {
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &list[i]);
	}
	int be, en, z;
	for (int i = 0; i < m; i++) {
		scanf("%d %d %d", &be, &en, &z);
		insert(be, en);
		if (z == 2) insert(en, be);
	}
	spfa(1);

	if (dis[n + N + N] == 0x3f3f3f3f || dis[n+N+N] >= 0) printf("0\n");
	else printf("%d\n", -dis[n + N + N]);
	return 0;
}

　　题解2：

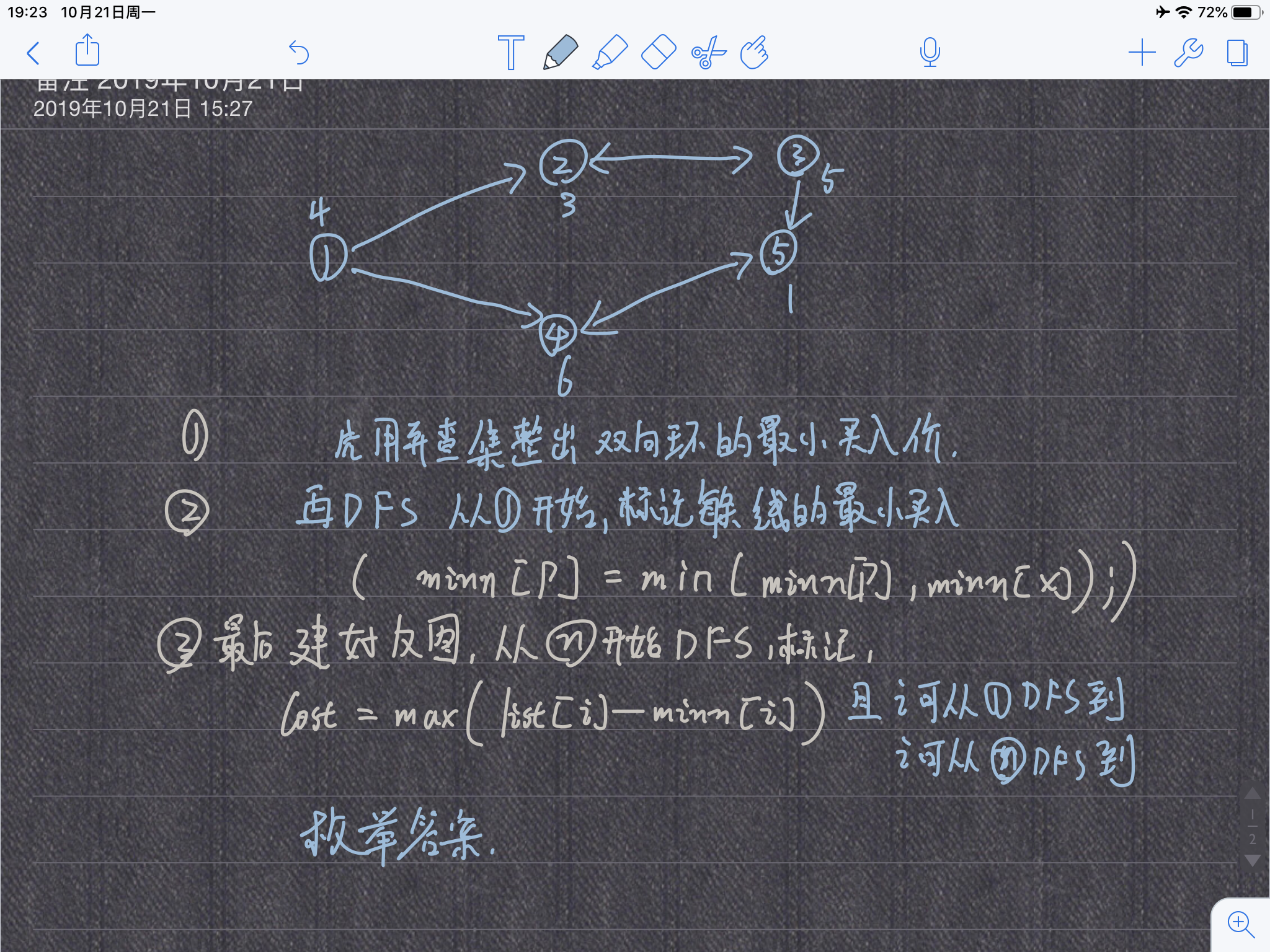
#include<cstring>
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
#define maxn 100010
using namespace std;
vector<int>G[maxn], G2[maxn];

void insert(int be, int en) {
	G[be].push_back(en);
}
void insert2(int be, int en) {
	G2[be].push_back(en);
}
int vis[maxn];
int list[maxn];
int vis2[maxn];
int n, m;
int minn[maxn];
int par[maxn];
int find(int x) {
	if (par[x] != -1) return par[x] = find(par[x]);
	else return x;
}
int dfs(int x) {

	if (vis[x]) return 0;
	vis[x] = 1;
	for (int i = 0; i < G[x].size(); i++) {
		int p = G[x][i];
		minn[p] = min(minn[p], minn[x]);
		dfs(p);
	}
	return 0;
}
int dfs2(int x) {

	if (vis2[x]) return 0;
	vis2[x] = 1;
	for (int i = 0; i < G2[x].size(); i++) {
		int p = G2[x][i];
		dfs2(p);
	}
	return 0;
}
int main() {
	memset(par, -1, sizeof(par));
	memset(vis, 0, sizeof(vis));
	memset(vis2, 0, sizeof(vis2));

	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &list[i]);
		minn[i] = list[i];
	}
	int be, en, z;
	for (int i = 0; i < m; i++) {
		scanf("%d%d%d", &be, &en, &z);
		insert(be, en);
		insert2(en, be);
		if (z == 2) {
			insert(en, be);
			insert2(be, en);
			int a = find(be);
			int b = find(en);
			if (a != b) {
				par[a] = b;
				minn[b] = min(minn[a], minn[b]);
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		int a = find(i);
		minn[i] = minn[a];
	}
	dfs(1);
	dfs2(n);
	if (!vis[n]) {
		printf("0\n");
		return 0;
	}
	int cns = 0;
	for (int i = 1; i <= n; i++) {

		if(vis[i] && vis2[i]) cns = max(cns, list[i] - minn[i]);
	}
	printf("%d\n", cns);
	return 0;
}