洛谷 P1242 新汉诺塔

原题链接

题目描述

设有n个大小不等的中空圆盘，按从小到大的顺序从1到n编号。将这n个圆盘任意的迭套在三根立柱上，立柱的编号分别为A、B、C，这个状态称为初始状态。

现在要求找到一种步数最少的移动方案，使得从初始状态转变为目标状态。

移动时有如下要求：

·一次只能移一个盘；

·不允许把大盘移到小盘上面。

输入输出格式

输入格式：

文件第一行是状态中圆盘总数；

第二到第四行分别是初始状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号；

第五到第七行分别是目标状态中A、B、C柱上圆盘的个数和从上到下每个圆盘的编号。

输出格式：

每行一步移动方案，格式为：move I from P to Q

最后一行输出最少的步数。

输入输出样例

输入样例#1：

5
3 3 2 1
2 5 4
0
1 2
3 5 4 3
1 1

输出样例#1：

move 1 from A to B
move 2 from A to C
move 1 from B to C
move 3 from A to B
move 1 from C to B
move 2 from C to A
move 1 from B to C
7

说明

圆盘总数≤45

每行的圆盘描述是从下到上的圆盘编号

题解

这道题目是经典的汉诺塔问题，没什么技术，但思维难度较高，如果条件判断太多则编码难度也会较高

首先，我们很容易想到一种假算法：（一定要注意它是错的，但对真算法有启发意义）

因为大盘子无法在小盘子上移动，而大盘子移动好之后又不会影响小盘子（这是本题所有操作的前提），故可以从大盘子开始移动。

我们从第N号盘子开始操作，计当前盘子为i号，如果它在原位置，那么就跳过，否则就将1~i-1号盘子都移动到不会动用的盘子，将目标盘子空出，然后将i号盘子放进去。经过N次操作，一定可以完成，但不能保证最优。

如图所示，如果我们要将第1号桩上的1个大盘子移到2号桩，那么我们就先将1、2号桩上所有比i号盘子小的盘子都移到第3号桩

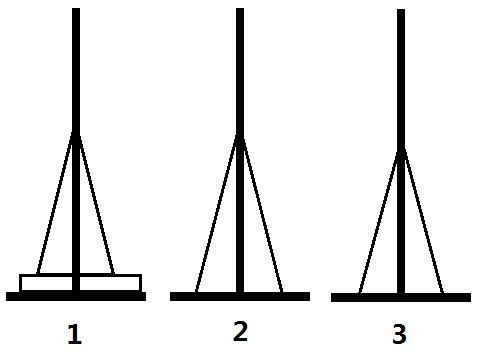
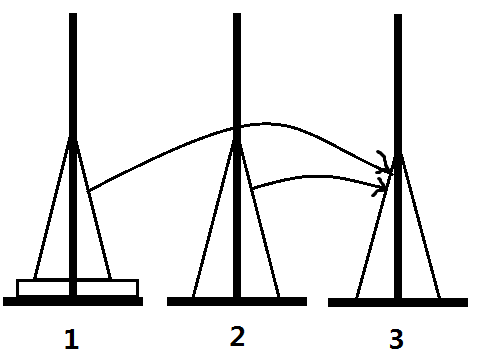
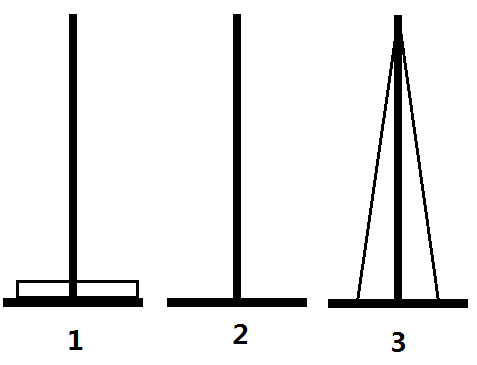
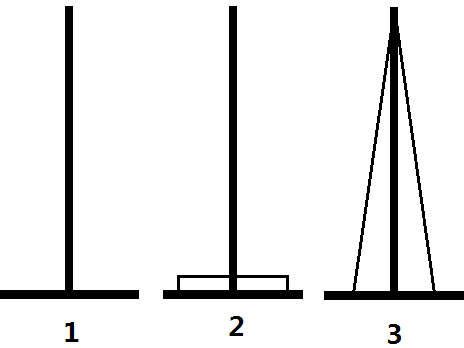
实现这一过程很简单，只要每次将1~i-1号盘子移动到闲置的位置，然后移动即可，代码也十分简单

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF=1e9+,MAXN=;
 int N,cur[MAXN],goal[MAXN],ans;
 char tran[]={' ','A','B','C'};/*translate*/
 inline void input(int *array,int opt){
     int ii,jj;
     scanf("%d",&ii);
     while(ii--){
         scanf("%d",&jj);
         array[jj]=opt;
     }
 }
 void dfs(int from/*from idx*/,int to/*to pos*/){/*move the "from"-th plate to position "to"*/
     if(cur[from]==to)
         return;
     int other=-cur[from]-to;
     for(int i=from-;i>=;i--)
         dfs(i,other);
     printf("move %d from %c to %c\n",from,tran[cur[from]],tran[to]);
     cur[from]=to;
     ans++;
 }
 int main(){
     scanf("%d",&N);
     input(cur,);
     input(cur,);
     input(cur,);
     input(goal,);
     input(goal,);
     input(goal,);

     for(int i=N;i>=;i--)
         dfs(i,goal[i]);
     printf("%d",ans);
     return ;
 }

但正如上面所说的，这是一个假算法。我们认定如图的变换方法是正确的，是建立在汉诺塔的性质的基础上的。在汉诺塔中，未归位的盘子都是连续叠加的（如下图1），不可能出现如图2的情况

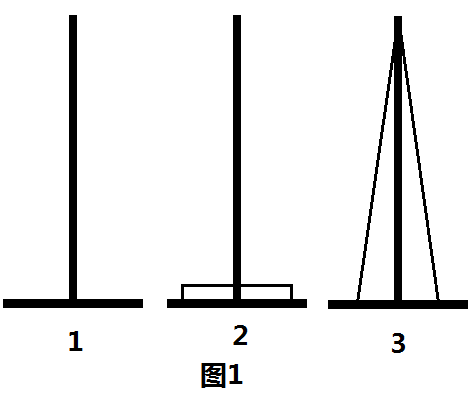
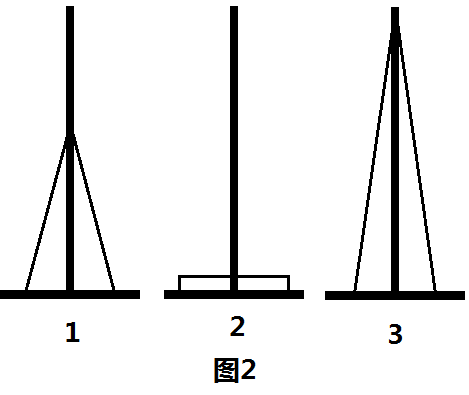
这样的话，无论将这个连续的塔从哪里移动到哪里都是等价的，故开始给出的假算法是成立的。

然而可惜的是，我们的塔最初是随机摆放的，所以会有另一种方法

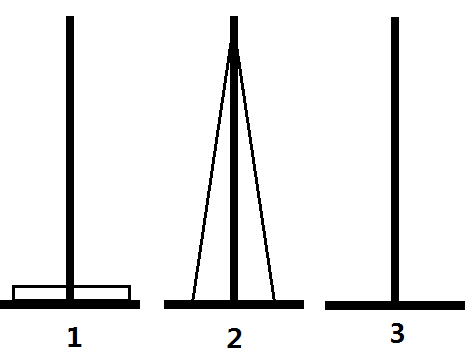
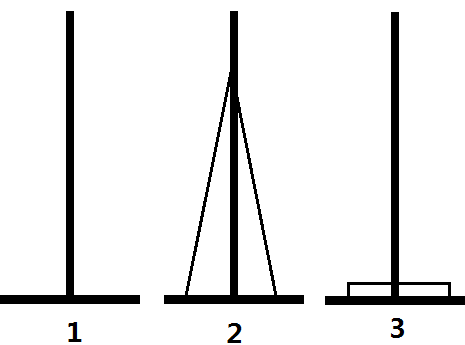
可以证明，没有其他移动方法了。但是否每次都要用两种方法呢？显然不是。观察两个图组可以发现，在进行了一次操作后，就还原到了汉诺塔的基本结构：一串连续的盘子，就可以用常规的方法操作了。

那图组2和图组1的过程又怎么实现呢？我们需要三种操作

1. move(idx,from,to):当1~idx在同一个桩子上时，将它们移到to号桩子
2. merge(idx,to):当1~idx不在同一个桩子上时，将它们移到to号桩子
3. solve(idx,to):当1~idx归位

move函数的实现很简单，递归将1~idx-1号盘子移到闲置的位置，将idx号盘子移到to，再将1~idx-1号盘子移到to即可

void mov(int idx,int from,int to,int other){
/*move 1~"idx"-th to "to"
in a heap*/
    if(!idx)
        return;
    mov(idx-,from,other,to);
    ans[st][++sz[st]]=(state){idx,from,to};
    mov(idx-,other,to,from);
}

merge函数也不难，将递归将1~idx-1号盘子移到闲置的位置（用merge），将idx号盘子移到to，再将1~idx-1号盘子移到to即可（用move）

void merg(int idx,int to){
/*move 1~"idx"-th to "to"
not in a heap*/
    if(!idx)
        return;
    if(cur[idx]==to)
        return merg(idx-,to);
    int other=-cur[idx]-to;
    merg(idx-,other);
    ans[st][++sz[st]]=(state){idx,cur[idx],to};
    mov(idx-,other,to,cur[idx]);
}

solve函数的思想同上

void solve(int idx,int to){
/*put 1-"idx"-th into its place*/
    if(!idx)
        return;
    if(goal[idx]==to)
        return solve(idx-,to);
    int other=-goal[idx]-to;
    mov(idx-,to,other,goal[idx]);
    ans[st][++sz[st]]=(state){idx,to,goal[idx]};
    solve(idx-,other);
}

有了这些操作，解题就很简单了，我们按照上面讲的两种情况分类，输出步数较少的方案即可

void work(int idx){
    if(!idx)
        return;
    if(cur[idx]==goal[idx])
        return work(idx-);
    int other=-cur[idx]-goal[idx];
    /*0:all to other, N to to*/
    st=;
    merg(idx-,other);
    ans[st][++sz[st]]=(state){idx,cur[idx],goal[idx]};
    solve(idx-,other);
    /*1:all to to, N to other, all to from, N to to*/
    st=;
    merg(idx-,goal[idx]);
    ans[st][++sz[st]]=(state){idx,cur[idx],other};
    mov(idx-,goal[idx],cur[idx],other);
    ans[st][++sz[st]]=(state) {idx,other,goal[idx]};
    solve(idx-,cur[idx]);
}

最终给出AC代码

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int INF=1e9+,MAXN=,MAXP=1e5;
 int N,cur[MAXN],goal[MAXN],cnt;
 char tran[]={'E','A','B','C'};/*translate*/
 inline void input(int *array,int opt){
     int ii,jj;
     scanf("%d",&ii);
     while(ii--){
         scanf("%d",&jj);
         array[jj]=opt;
     }
 }
 struct state{ int idx,from,to; }ans[][MAXP];
 int st,sz[];
 void mov(int idx,int from,int to,int other){
 /*move 1~"idx"-th to "to"
 in a heap*/
     if(!idx)
         return;
     mov(idx-,from,other,to);
     ans[st][++sz[st]]=(state){idx,from,to};
     mov(idx-,other,to,from);
 }
 void merg(int idx,int to){
 /*move 1~"idx"-th to "to"
 not in a heap*/
     if(!idx)
         return;
     if(cur[idx]==to)
         return merg(idx-,to);
     int other=-cur[idx]-to;
     merg(idx-,other);
     ans[st][++sz[st]]=(state){idx,cur[idx],to};
     mov(idx-,other,to,cur[idx]);
 }
 void solve(int idx,int to){
 /*put 1-"idx"-th into its place*/
     if(!idx)
         return;
     if(goal[idx]==to)
         return solve(idx-,to);
     int other=-goal[idx]-to;
     mov(idx-,to,other,goal[idx]);
     ans[st][++sz[st]]=(state){idx,to,goal[idx]};
     solve(idx-,other);
 }
 void work(int idx){
     if(!idx)
         return;
     if(cur[idx]==goal[idx])
         return work(idx-);
     int other=-cur[idx]-goal[idx];
     /*0:all to other, N to to*/
     st=;
     merg(idx-,other);
     ans[st][++sz[st]]=(state){idx,cur[idx],goal[idx]};
     solve(idx-,other);
     /*1:all to to, N to other, all to from, N to to*/
     st=;
     merg(idx-,goal[idx]);
     ans[st][++sz[st]]=(state){idx,cur[idx],other};
     mov(idx-,goal[idx],cur[idx],other);
     ans[st][++sz[st]]=(state) {idx,other,goal[idx]};
     solve(idx-,cur[idx]);
 }
 int main(){
     scanf("%d",&N);
     input(cur,);
     input(cur,);
     input(cur,);
     input(goal,);
     input(goal,);
     input(goal,);

     work(N);

     for(int i=,ed=min(sz[],sz[]),j=sz[]>sz[];i<=ed;i++)
         printf("move %d from %c to %c\n",ans[j][i].idx,tran[ans[j][i].from],tran[ans[j][i].to]);
     printf("%d",min(sz[],sz[]));
     return ;
 }