OpenCASCADE点向直线投影
OpenCASCADE点向直线投影
在GeomLib_Tool类中提供了计算指定点在曲线、曲面上的参数，这个算法具有通用性，即对任意曲线、曲面来反求点的参数。
本文主要结合源码分析点向直线投影的算法。在类Extrema_ExtPElC中提供了点向基本的曲线距离极值计算的功能，基本曲线就是常见的直线、圆、椭圆、抛物线、双曲线等。其中点到直线的距离源码如下：
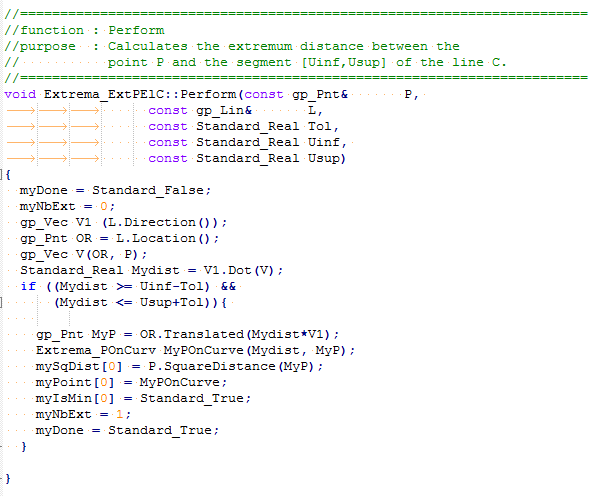
根据源码的意思画出一个图来说明会更直观，其中向量V1是直线的方向向量，V是直线的起点到点P的向量。
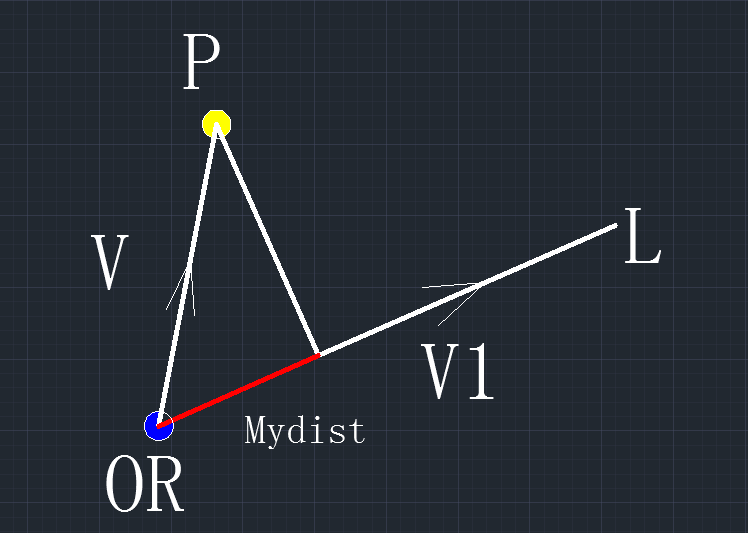
算法主要使用向量点乘得到点投影到直线上的距离Mydist，再将点OR沿着直线的方向V1移动Mydist距离就得到了点投影到直线上的点。结合源码及其注释还可以看出只有点在直线的投影点到直线原点OR的距离Mydist在指定的范围内才会保存计算结果。当有范围限制时，即是计算的点到线段的投影，无限制时就是点到直线的投影。
向量的计算有时可以简化程序而且算法性能高，充分理解向量的运算并熟练地运用是图形学编程中的基础。
OpenCASCADE点向直线投影的更多相关文章
- OpenCASCADE点向平面投影
OpenCASCADE点向平面投影 OpenCASCADE的ProjLib类提供了解析曲线(直线.圆.椭圆.抛物线.双曲线)向解析曲面(平面.圆柱面.圆锥面.球面.圆环面)投影的功能,主要用来计算三维 ...
- OpenCASCADE圆与平面求交
OpenCASCADE圆与平面求交 eryar@163.com 在 解析几何求交之圆与二次曲面中分析了OpenCASCADE提供的类IntAna_IntConicQuad可以用来计算圆与二次曲面之间的 ...
- Two analytical 2d line intersection in OpenCASCADE
Two analytical 2d line intersection in OpenCASCADE eryar@163.com Abstract. OpenCASCADE geometric too ...
- PCA算法详解——本质上就是投影后使得数据尽可能分散（方差最大），PCA可以被定义为数据在低维线性空间上的正交投影，这个线性空间被称为主⼦空间（principal subspace），使得投影数据的⽅差被最⼤化（Hotelling, 1933），即最大方差理论。
PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...
- Intersection between a 2d line and a conic in OpenCASCADE
Intersection between a 2d line and a conic in OpenCASCADE eryar@163.com Abstract. OpenCASCADE provid ...
- 数据降维技术（1）—PCA的数据原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- 线性代数和numpy——黑板客老师课程学习
一.代数是什么 代数->数的抽象表示->向量空间(线性空间) 线代->线性代数 关系: 向量空间之间和内部转换是通过线性变换. 实数——一维空间的点 复数——二维空间的点 如果两个向 ...
- PCA原理与实践
在对数据进行预处理时,我们经常会遇到数据的维数非常之大,如果不进行相应的特征处理,那么算法的资源开销会很大,这在很多场景下是我们不能接受的.而对于数据的若干维度之间往往会存在较大的相关性,如果能将数据 ...
- PCA的数学原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维 数据的 ...
随机推荐
- callable接口的多线程实现方式
package com.cxy.juc; import java.util.concurrent.Callable; import java.util.concurrent.ExecutionExce ...
- Qt学习笔记----信号与槽实现的四种方式
1.以按钮为例,首先添加一个按钮,对象名为pushButton,在按钮是右键单击选择“转到槽”即可,在转到槽选择面板(右图)里面选择需要进行的操作,比如单击clicked() 2.选择菜单“编辑”,找 ...
- js获取table checkbox选中行的值.mdjs获取table checkbox选中行的
<!DOCTYPE html> <html> <head> <script src="https://cdn.staticfile.org/jque ...
- ionic js 加载动画 ionSpinner 提供了许多种旋转加载的动画图标。当你的界面加载时，你就可以呈现给用户相应的加载图标。 该图标采用的是SVG
ionic 加载动画 ion-spinner ionSpinner 提供了许多种旋转加载的动画图标.当你的界面加载时,你就可以呈现给用户相应的加载图标. 该图标采用的是SVG. 用法 <ion- ...
- APB简介
一.血缘 AMBA: Advanced Microcontroller Bus Architecture 高级处理器总线架构 AHB: Advanced High-performance Bus 高级 ...
- 【JZOJ6287】扭动的树
description analysis 区间\(DP\),首先按照键值排个序,这样保证树的中序遍历就为原序列 设\(f[0][i][j]\)表示\([i..j]\)区间作为\([unknown..i ...
- 线性dp，后缀处理——cf1016C好题
绝对是好题 #include<bits/stdc++.h> using namespace std; #define maxn 300005 #define ll long long ll ...
- MFC打开/保存文件对话框:CFileDialog
MFC打开/保存文件对话框:CFileDialog CFileDialog 文件选择对话框的使用:首先构造一个对象并提供相应的参数,构造函数原型如下: CFileDialog::CFileDial ...
- LUOGU P4159 [SCOI2009]迷路(矩阵乘法)
传送门 解题思路 以前bpw讲过的一道题,顺便复习一下矩阵乘法.做法就是拆点,把每个点拆成\(9\)个点,然后挨个连边.之后若\(i\)与\(j\)之间的边长度为\(x\),就让\(i\)的第\(x\ ...
- SSM14-通过AOP实现日志记录
1.要求使用AOP思想,实现对每一个用户登陆后,将以下信息保存在数据库 1>登陆时间 2>退出时间 3>登录的IP地址 4>访问点URL(访问了那些Controller) 5& ...