paper: VG -- re-read

重点: 

1.The constructed graph inherits several properties of the series in its structure.

periodic series --> regular graphs这句话是错的,periodic series 转化成的图并不是regular graphs, 转化成的图的degree distribution是分形的. fractal series --> scale-free networks. random series --> random graph.

此图为100个10周期的随机数形成的图,而得到的每个结点的度分布图表.

图表示乱七八糟,不可解释,但是图的度曲线具有统计意义,在统计上具有一定的规律.

2. characterize time series from a new point of view in the complex network theory (node, link).

目前转换成的图是random graphs, 符合泊松分布；characterize energy consumption from a new point of view.

3. properties of VG: connected临近节点总是相连; undirected; invariant under affine traformations仿射变换下的不变性.

评论: 里面水很深,需要学习大量的知识. 复杂网络,复杂系统.

Basic knowledge: 

1. what is a random graph and scale-free graph.

random graph的度分布, 钟型曲线, 符合泊松分布poisson distribution；scale-free graph的degree distribution 符合幂律分布pow-law distribution；

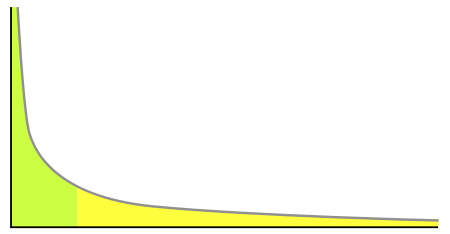An example power-law graph, being used to demonstrate ranking of popularity. To the right is the long tail, and to the left are the few that dominate (also known as the 80–20 rule).

node, link 的表述是网络理论中的; vertex (vertices) and edge是数学中图论的表述.

在网络理论中，无尺度网络（Scale-free network，或称无标度网络）是带有一类特性的复杂网络，其典型特征是在网络中的大部分节点只和很少节点连接，而有极少的节点与非常多的节点连接。这种关键的节点（称为“枢纽”或“集散节点”）的存在使得无尺度网络对意外故障有强大的承受能力，但面对协同性攻击时则显得脆弱。现实中的许多网络都带有无尺度的特性，例如因特网、金融系统网络、社会人际网络等等。

自二十世纪60年代开始，对复杂网络的研究主要集中在随机网络上。随机网络，又称随机图，是指通过随机过程制造出的复杂网络。最典型的随机网络是保罗·埃尔德什和阿尔弗雷德·雷尼提出的ER模型。ER模型是基于一种“自然”的构造方法：假设有个节点，并假设每对节点之间相连的可能性都是常数。这样构造出的网络就是ER模型网络。科学家们最初使用这种模型来解释现实生活中的网络^[1]:7-9。

在一般的随机网络（如ER模型）中，大部分的节点的度都集中在某个特殊值附近，成钟形的泊松分布规律（见图3）^[3]。偏离这个特定值的概率呈指数性下降，远大于或远小于这个值的可能都是微乎其微的^[2]:11，就如一座城市中成年居民的身高大致的分布一样。然而在1998年，Albert-László Barabási、Réka Albert等人合作进行一项描绘万维网的研究时，发现通过超链接与网页、文件所构成的万维网网络并不是如一般的随机网络一样，有着均匀的度分布^[4][5]。他们发现，万维网是由少数高连接性的页面串联起来的。绝大多数（超过80%）的网页只有不超过4个超链接，但极少数页面（不到总页面数的万分之一）却拥有极多的链接，超过1000个，有一份文件甚至与超过200万个其他页面相连。与居民身高的例子作类比的话，就是说大多数的节点都是“矮个子”，而却又有极少数的身高百丈的“巨人”。Barabási等人将其称为“无尺度”网络^[4]。

2. 幂函数与指数函数的区别

3. visibility graph theory

可见性图（Visibility Graph）算法是计算几何中的基础算法，该算法解决n维空间中的多个图形的每个顶点与其他顶点之间的可见性问题。所谓“可见性”，即图中任意两个顶点的连线不会与图中其他边相交，也就是说这两个点之间没有阻碍。

Visibility Graph是将起始节点，所有障碍物的顶点和目标节点相互连接来构建路线图

所有两个节点间的连线，不能碰到障碍物

在建立可视化图表后，可以应用搜索算法来查找从开始到目标的最短路径。

me: 可以将time series想象为一个障碍物,这样VG的含义就大了, The visibility graph of a set of locations that lie in a line can be interpreted as a graph-theoretical representation of a time series.^[2] This particular case builds a bridge between time series, dynamical systems and graph theory.

4. regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other.^[1] A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.

5. 复杂系统,复杂网络.

新英格兰复杂系统研究所长文综述：复杂系统科学及其应用