面向对象的封装、继承和多态特性_python

一、面向对象的几个特点

面向对象也称为类，拥有下面几个特点

1、封装特性：利用类的__init__(self)构造方法封装对象

构造方法：__init__(self)：在生成对象的时候会自动调用

例子：

class person():
    def __init__(self,name,age,sex):
        self.name=name
        self.age=age
        self.sex=sex
    def print_info(self,num):
        print(num,self.name,self.age, self.sex)

obj=person("chen",21,'男')  #调用类生成对象时填写的参数就是__init__()方法的参数。生成对象时填写的参数就是构造方法的参数
obj.print_info(1)
obj2=person("xiao",22,'女') #封装的第二个对象
obj2.print_info(2)

2、继承
（1）建立父子关系：

class father:
    def backetball(self):
        print('backetball')

    def football(self):
        print('father_football')

class son(father):   #指定这个类的父类，与其他类产生父子关系
    def football(self):
        print("football")
obj=son()　　　　　　　　#生成子类对象
obj.football()  #football  #当子类与父类拥有同一个方法时，默认只执行子类的方法
obj.backetball()    #backetball  #可以调用父类中的方法

①如果子类和父类有相同的方法，默认只执行子类中的，如何也要执行父类中的？
在子类的方法中添加：
super（子类名，self）.方法（...）

class son(father):   
    def football(self):
        super(son,self).football()  #添加之后也会执行父类的方法，凡是子类也是会执行
        print("football")

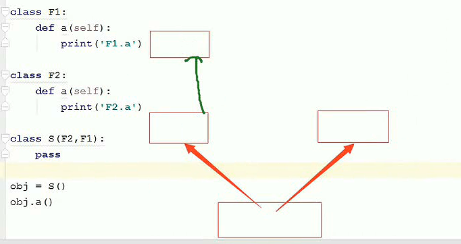
（2）多继承（一个子类多个父类）
　　

　　①出现调用父类方法时，父类中有相同的方法，调用顺序：

　　从左到右（如上列子F2优先于F1），一条路走到黑；同一个根时，根最后才执行。

　　②默认只执行一个_init_方法，如果要执行多个，可以在第一个里面进行调用其他

　　如下面流转执行顺序例子：

　　

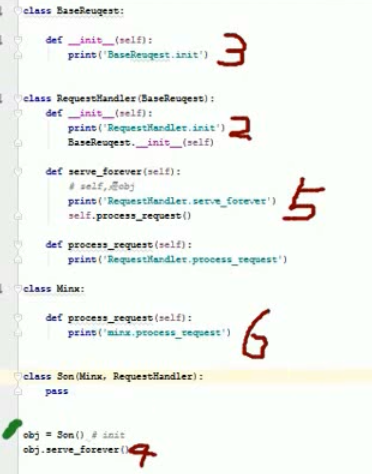
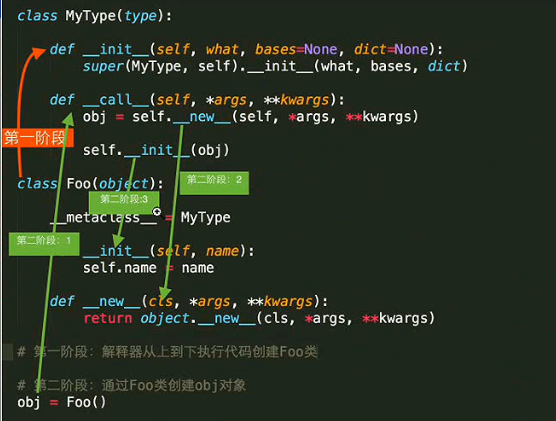
更深知识点：

　　类都是type类的对象，类生成对象时不是单纯执行__init__,还有type类里面的__call__和__new___，最终展示出来就是执行了__init__方法,其实是执行了好几个方法。

 3、多态

一个接口，多种实现

生活例子：老板只需要说开始工作，各部门就会开始各自工作