小小知识点(三十九) 正交频分复用OFDM的基本原理及实现
引言
符号间干扰(ISI)是无线传输系统设计中需要考虑的因素,采用什么样的处理方法取决于数据传输速率或等效传输带宽来决定
(1)若数据速率低且与信道最大延迟相比符号持续时间较长,那么就可能无需任何均衡技术处理ISI
(2)若数据速率或通信距离增加,ISI变得越来越严重,如数据以100Mb/s的速率在最大延迟为10us的信道上传输,那么ISI将扩展100个符号,这时就必须借助均衡技术。另外,OFDM技术提供了让数据以较高的速率在较大延迟的信道上传输的另一种途径。
OFDM的基本思想
把一个高速率的数据流分解成许多低速率的子数据流以并行方式在许多子信道上传输。
OFDM的基本原理
注:离散傅里叶变换公式,源自《The descret fourier transfer theorys algorithms applications 》by D.Sundararajan
IDFT
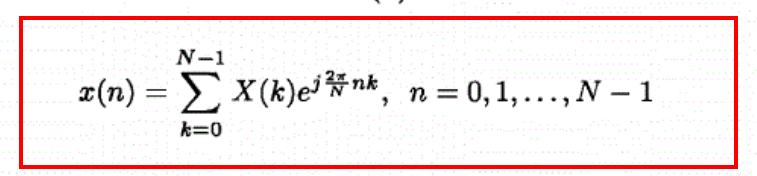
DFT
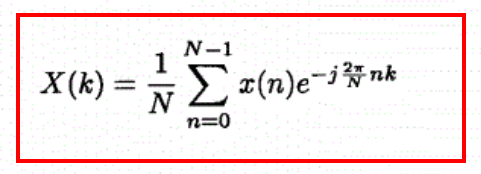
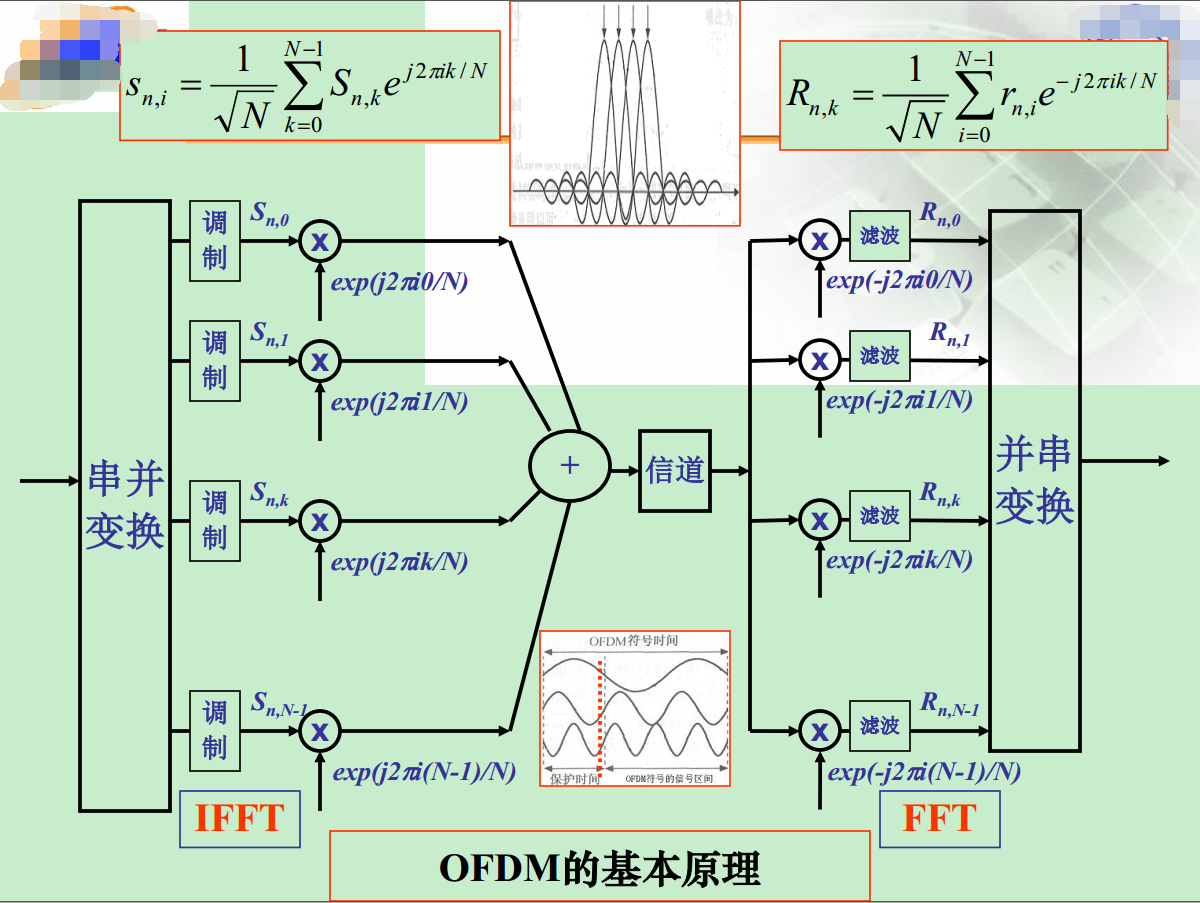
其中Sn,k是映射的IQ复信号
(注:详细的说明见《宽带无线通信》中的第四部分OFDM)
保护间隔和循环前缀
OFDM把输入的高速率数据流串并转换到N个并行的子信道中,使得每个用于调制子载波的数据符号周期扩大为原始数据符号周期的N倍,时延扩展与符号周期的比值同样也降低N倍。
GI:为最大限度的消除符号间干扰ISI,可以在每个OFDM信号块之间插入保护间隔(Guard Interval,GI),而且该保护间隔长度Tg一般要大于无线信道的最大时延扩展,这样一个符号的多径分量就不会对下一个符号造成干扰。
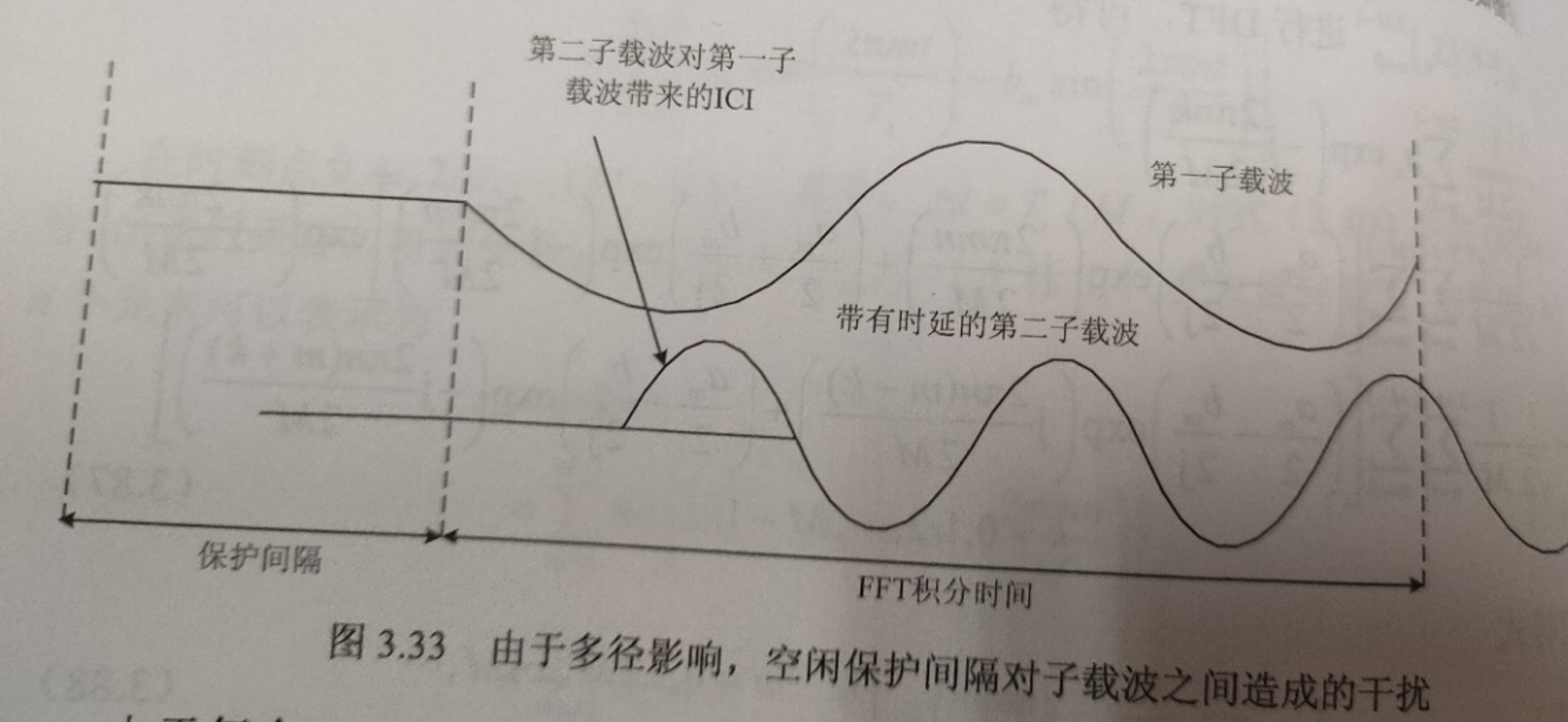
CP:当保护间隔内,不插入任何信号,即是一段空闲的传输时段。然而在这种情况下,由于多径传播的影响,则会产生信道间干扰(ICI),即子载波间的正交性遭到破坏,不同的子载波之间产生干扰。为消除多径造成的ICI,OFDM符号需要在保护间隔内插入循环前缀(cycle prefix,CP)
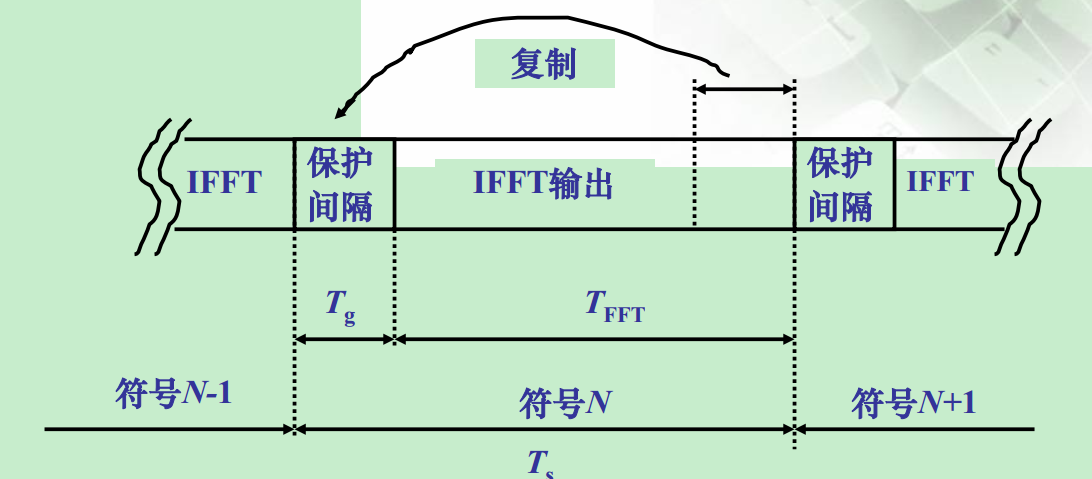
CP可以充当保护间隔,从而消除ISI。因为它的存在使得前一个符号多径的副本都落在后一个符号的CP范围内,从而消除两个符号间的干扰;由于OFDM符号的一部分呈现周期性,将信号与信道冲击响应的线性卷积转换成循环卷积,个子载波将保持正交性,从而防止ICI。
OFDM的基本参数的选择

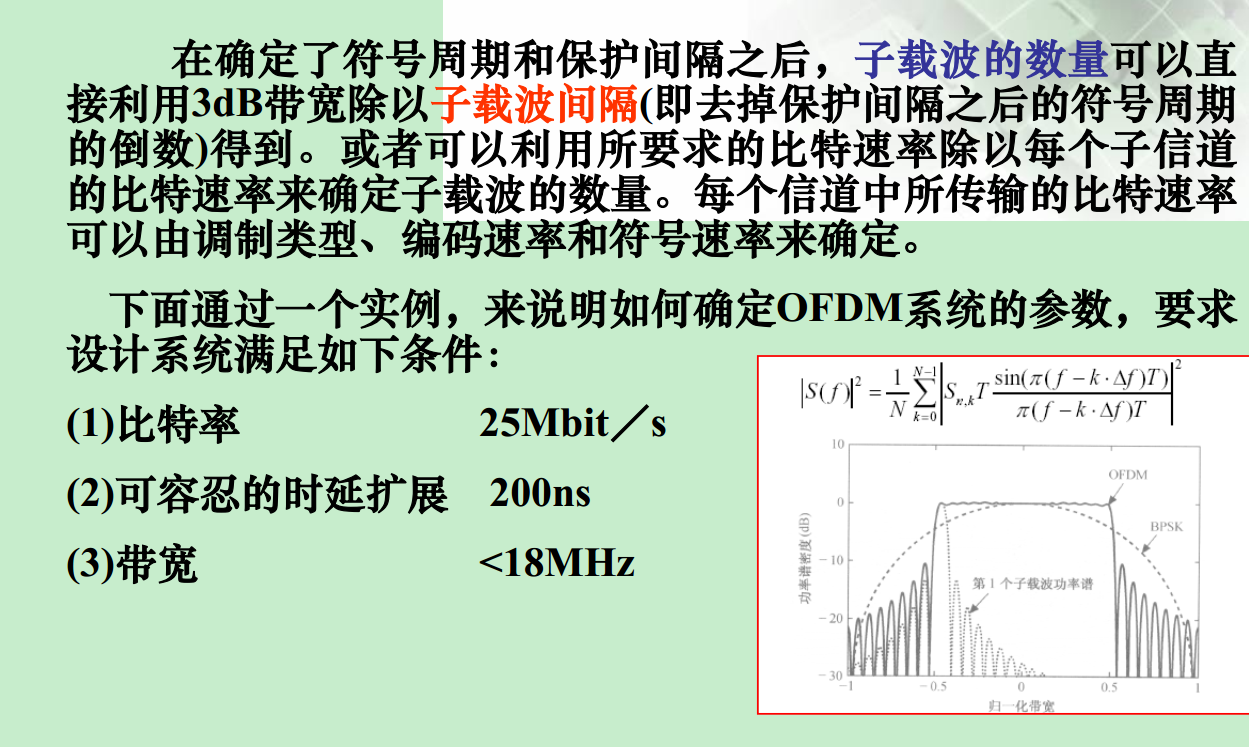


小小知识点(三十九) 正交频分复用OFDM的基本原理及实现的更多相关文章
- centos shell编程5 LANMP一键安装脚本 lamp sed lnmp 变量和字符串比较不能用-eq cat > /usr/local/apache2/htdocs/index.php <<EOF重定向 shell的变量和函数命名不能有横杠 平台可以用arch命令,获取是i686还是x86_64 curl 下载 第三十九节课
centos shell编程5 LANMP一键安装脚本 lamp sed lnmp 变量和字符串比较不能用-eq cat > /usr/local/apache2/htdocs/ind ...
- 对正交频分复用OFDM系统的理解
OFDM系统 正交频分复用OFDM(Orthogonal Frenquency Division Multiplexing)是一种多载波调制技术. 基本思想:在发送端,它将高速串行数据经过串并变换形成 ...
- NeHe OpenGL教程 第三十九课:物理模拟
转自[翻译]NeHe OpenGL 教程 前言 声明,此 NeHe OpenGL教程系列文章由51博客yarin翻译(2010-08-19),本博客为转载并稍加整理与修改.对NeHe的OpenGL管线 ...
- Java进阶(三十九)Java集合类的排序,查找,替换操作
Java进阶(三十九)Java集合类的排序,查找,替换操作 前言 在Java方向校招过程中,经常会遇到将输入转换为数组的情况,而我们通常使用ArrayList来表示动态数组.获取到ArrayList对 ...
- Gradle 1.12用户指南翻译——第三十九章. IDEA 插件
本文由CSDN博客万一博主翻译,其他章节的翻译请参见: http://blog.csdn.net/column/details/gradle-translation.html 翻译项目请关注Githu ...
- SQL注入之Sqli-labs系列第三十八关、第三十九关,第四十关(堆叠注入)
0x1 堆叠注入讲解 (1)前言 国内有的称为堆查询注入,也有称之为堆叠注入.个人认为称之为堆叠注入更为准确.堆叠注入为攻击者提供了很多的攻击手段,通过添加一个新 的查询或者终止查询,可以达到修改数据 ...
- 第三百三十九节,Python分布式爬虫打造搜索引擎Scrapy精讲—Scrapy启动文件的配置—xpath表达式
第三百三十九节,Python分布式爬虫打造搜索引擎Scrapy精讲—Scrapy启动文件的配置—xpath表达式 我们自定义一个main.py来作为启动文件 main.py #!/usr/bin/en ...
- “全栈2019”Java第三十九章:构造函数、构造方法、构造器
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...
- WPF,Silverlight与XAML读书笔记第三十九 - 可视化效果之3D图形
原文:WPF,Silverlight与XAML读书笔记第三十九 - 可视化效果之3D图形 说明:本系列基本上是<WPF揭秘>的读书笔记.在结构安排与文章内容上参照<WPF揭秘> ...
随机推荐
- uva 10253 Series-Parallel Networks (整数划分+多重集)
UVa Online Judge 题意是计算给定数量的边通过串联并联两种方式,能组成多少种不同的网络.将它转化为一个树形结构,也就是求有多少不同构的树. 代码如下: #include <cstd ...
- Websocket 群聊功能
websocket 群聊 前提关闭防火墙 写入代码 from flask import Flask,request,render_template from geventwebsocket.handl ...
- Hibernate懒加载导致json数据对象传输异常的问题---(非常重要)
1. 异常: [console_demo][WARN] [2016-12-15 19:49:35] org.springframework.web.servlet.mvc.support.Defaul ...
- H3C 主机单播IP包发送
- oracle 用EXISTS替换DISTINCT
当提交一个包含一对多表信息(比如部门表和雇员表)的查询时,避免在SELECT子句中使用DISTINCT. 一般可以考虑用EXIST替换 例如: 低效: SELECT DISTINCT DEPT_NO, ...
- xUtils框架的介绍(三)
接上回,继续介绍xUtils的最后两个模块:DbUtils和HttpUtils.首先先介绍第一个SQLite数据库操纵的简单ORM框架,只要能理解xUtils为我们提供的api,相信你也能熟练的把Db ...
- Unity5.6.4f1 配置WebGL教程
Unity 5.6.4f1 发布WebGL的配置教程 步骤一:先查看自带的Unity是否yi配置好WebGL的项,若无,则可遵循以下教程来设置 步骤二:下图是我已经设置好的,未设置好的状态是,有个Op ...
- input 的 pattern 验证表单
pattern 用于定义验证输入正则表达式 pattern 属性适用于以下 <input> 类型:text, search, url, telephone, email 以及 passwo ...
- java线程与进程的比较
线程具有许多传统进程所具有的特征,故又称为轻型进程(Light—Weight Process)或进程元:而把传统的进程称为重型进程(Heavy—Weight Process),它相当于只有一个线程的任 ...
- P1063 高兴的津津
题目描述 津津上高中了.她在自己的妈妈的魔鬼训练下,成为了一个神犇,每次参加一次OI比赛必拿Au虐全场.每次她拿到一个Au后就很高兴.假设津津不会因为其它事高兴,并且她的高兴会持续T天(包包含获奖当天 ...
