二叉树的详细实现 (C++)

二叉树的定义

    以递归形式给出的：一棵二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。二又树的特点是每个结点最多有两个子女，分别称为该结点的左子女和右子女。在二又树中不存在度大于2的结点，并且二又树的子树有左、右之分，其子树的次序不能颠倒。二又树是分支数最大不超过2的有根有序树。它可能有5种不同的形态。

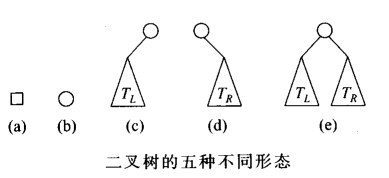
二叉树的性质

 

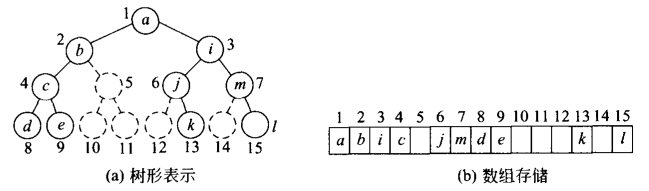
二叉树的数组存储方式

 

遇到空子树，应在编号时假定有此子树进行编号，而在顺序存储时当作有此子树那样把位置留出来。这样才能反映二叉树结点之间的相互关系，由其存储位置找到它的父结点、子女、兄弟结点的位置。但这样做有可能会消耗大量的存储空间。例如：单支二叉树，会浪费很多空间。

 

如果根节点编号是从1开始有有以下结论：

    中间节点一定在倒数第二层，最后一个节点的数就是总节点的个数，总结点数除2就是中间节点的数的个数，父节点的节点数*2<总节点个数，当前节点一定有两个孩子，如果=就只有一个孩子，如果<就没有一个孩子。

二叉树的链表存储表示

 

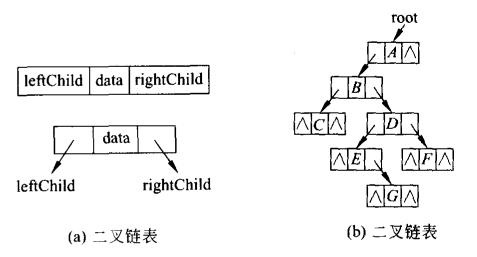
二叉树结点类型的定义

 template<typename T>
 struct BinTreeNode
 {
     T data;    //结点中存储的数据
     BinTreeNode<T> *leftChild, *rightChild;    //左子树和右子树
     BinTreeNode() :leftChild(NULL), rightChild(NULL) {}    //无参构造函数
     BinTreeNode(T x, BinTreeNode<T> *l = NULL, BinTreeNode<T> *r = NULL) :data(x), leftChild(l), rightChild(r) {}    //带默认值的有参构造参数
 };

二叉树的基本框架

//二叉树

//结点类型
template <typename T>
struct BinTreeNode
{
    T data;                                                                                                        //结点中存储的数据
    BinTreeNode<T> *leftChild, *rightChild;                                                                        //左子树和右子树
    BinTreeNode() : leftChild(NULL), rightChild(NULL) {}                                                           //无参构造函数
    BinTreeNode(T x, BinTreeNode<T> *l = NULL, BinTreeNode<T> *r = NULL) : data(x), leftChild(l), rightChild(r) {} //带默认值的有参构造参数
};

//二叉树类
template <typename T>
class BinaryTree
{
public:

//==========二叉树构造与析构==========//

    //构造函数
    BinaryTree() : root(NULL) {}

    //指定结束标志的构造函数
    BinaryTree(T value) : RefValue(value), root(NULL) {}

    //析构函数
    ~BinaryTree() { Destroy(root); }

//==========二叉树的创建==========//

    //使用广义表创建二叉树，以'#'字符代表结束
    void CreateBinTree() { CreateBinTree(root); }

    //前序遍历创建二叉树(前序遍历的应用)，用#表示空结点
    void CreateBinTree_PreOrder() { CreateBinTree_PreOrder(root); }

    //使用先序遍历和中序遍历创建二叉树
    void CreateBinTreeBy_Pre_In(const char *pre, const char *in)
    {
        int n = strlen(pre);
        CreateBinTreeBy_Pre_In(root, pre, in, n);
    }

    //使用后序遍历和中序遍历创建二叉树
    void CreateBinTreeBy_Post_In(const char *post, const char *in)
    {
        int n = strlen(post);
        CreateBinTreeBy_Post_In(root, post, in, n);
    }

//==========二叉树的遍历==========//

    //先序遍历（递归）
    void PreOrder() { PreOrder(root); }

    //中序遍历(递归)
    void InOrder() { InOrder(root); }

    //后序遍历（递归）
    void PostOrder() { PostOrder(root); }

    //先序遍历(非递归)
    void PreOrder_NoRecurve() { PreOrder_NoRecurve(root); }

    //中序遍历(非递归)
    void InOrder_NoRecurve() { InOrder_NoRecurve(root); }

    //后序遍历(非递归)
    void PostOrder_NoRecurve() { PostOrder_NoRecurve(root); }

    //层次遍历(非递归)
    void LevelOrder() { LevelOrder(root); }

//==========获取结点==========//

    //获取二叉树的根节点
    BinTreeNode<T> *getRoot() const
    {
        return root;
    }

    //获取current结点的父节点
    BinTreeNode<T> *Parent(BinTreeNode<T> *current)
    {
        return (root == NULL || root == current) ? NULL : Parent(root, current); //如果没有根节点或current结点就是root结点，就没有父节点
    }

    //获取current结点的左结点
    BinTreeNode<T> *LeftChild(BinTreeNode<T> *current)
    {
        return (current != NULL) ? current->leftChild : NULL;
    }

    //获取current结点的右结点
    BinTreeNode<T> *RightChild(BinTreeNode<T> *current)
    {
        return (current != NULL) ? current->rightChild : NULL;
    }

//==========成员函数==========//

    //销毁函数
    void Destroy() { Destroy(root); }

    //拷贝二叉树(前序遍历的应用)
    BinaryTree(BinaryTree<T> &s)
    {
        root = Copy(s.getRoot());
    }

    //判断两颗二叉树是否相等(前序遍历的应用)
    bool operator==(BinaryTree<T> &s)
    {
        return (equal(this->getRoot(), s.getRoot()));
    }

    //计算二叉树的结点的个数(后序遍历的应用)
    int Size() { return Size(root); }

    //计算二叉树的高度（后序遍历的应用）
    int Height() { return Height(root); }

    //判断二叉树是否为空
    bool Empty() { return (root == NULL) ? true : false; }

    //以广义表的形式输出二叉树(前序遍历的应用)
    void PrintBinTree() { PrintBinTree(root); }

private:
    BinTreeNode<T> *root; //根节点
    T RefValue;           //数据输入停止的标志，需要一个构造函数
};

二叉树的创建

　　1.使用广义表创建

从广义表A（B（D，E（G，）），C（，F））# 建立起来的二叉树。

 

算法基本思路：

　　1.若是字母（假定以字母作为结点的值），则表示是结点的值，为它建立一个新的结点，并把该结点作为左子女（当k=1）或右子女（当k=2）链接到其父结点上。

　　2.若是左括号"("，则表明子表的开始，将k置为1；若遇到的是右括号")"，则表明子表结束。

　　3.若遇到的是逗号","，则表示以左子女为根的子树处理完毕，应接着处理以右子女为根的子树，将k置为2。如此处理每一个字符，直到读入结束符“#”为止。

在算法中使用了一个栈s，在进入子表之前将根结点指针进栈，以便括号内的子女链接之用。在子表处理结束时退栈。

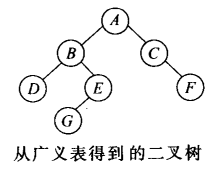
     //使用广义表创建二叉树函数,这里以“字符”创建二叉树,以'#'字符代表结束
     void CreateBinTree(BinTreeNode<T>* &BT)
     {
         stack< BinTreeNode<T>* > s;
         BT = NULL;
         BinTreeNode<T> *p, *t;    //p用来记住当前创建的节点，t用来记住栈顶的元素
         int k;    //k是处理左、右子树的标记
         T ch;
         cin >> ch;

         while (ch != RefValue)
         {
             switch (ch)
             {
             case '(':    //对(做处理
                 s.push(p);
                 k = ;
                 break;

             case ')':    //对)做处理
                 s.pop();
                 break;

             case ',':    //对,做处理
                 k = ;
                 break;

             default:
                 p = new BinTreeNode<T>(ch);    //构造一个结点
                 if (BT == NULL)    //如果头节点是空
                 {
                     BT = p;
                 }
                 else if (k == )    //链入*t的左孩子
                 {
                     t = s.top();
                     t->leftChild = p;
                 }
                 else    //链入*t的右孩子
                 {
                     t = s.top();
                     t->rightChild = p;
                 }
             }
             cin >> ch;
         }
     }

　　2.使用已知的二叉树的前序遍历创建

　　必须对应二又树结点前序遍历的顺序，并约定以输入序列中不可能出现的值作为空结点的值以结束递归，此值通过构造函数存放在RefValue中。例如用“#”或表示字符序列或正整数序列空结点。

 

　　前序遍历所得到的前序序列为ABC##DE#G##F###。

算法的基本思想是：

　　每读入一个值，就为它建立结点。该结点作为根结点，其地址通过函数的引用型参数subTree直接链接到作为实际参数的指针中。然后，分别对根的左、右子树递归地建立子树，直到读入“#”建立空子树递归结束。

     //创建二叉树(利用已知的二叉树的前序遍历创建)用#表示空结点
     void CreateBinTree_PreOrder(BinTreeNode<T>* &subTree)
     {
         T item;
         if (cin >> item)
         {
             if (item != RefValue)
             {
                 subTree = new BinTreeNode<T>(item);    //构造结点
                 if (subTree == NULL)
                 {
                     cout << "空间分配错误！" << endl;
                     exit();
                 }
                 CreateBinTree_PreOrder(subTree->leftChild);    //递归创建左子树
                 CreateBinTree_PreOrder(subTree->rightChild);    //递归创建右子树
             }
             else
             {
                 subTree == NULL;
             }
         }
     }

3.根据已知的前序遍历和中序遍历创建二叉树

根据前序遍历，先找到这棵树的根节点，也就是数组受中第一个结点的位置，创建根节点。

然后在中序遍历中找到根的值所在的下标，切出左右子树的前序和中序

注意：如果前序遍历的数组长度为0，说明是一棵空树。

举例：

首先可以确定A是这棵树的根节点，然后根据中序遍历切出A的左右子树，得到BCD属于A的左子树，E属于A的右子树，如下图：

接着以B为根节点，在中序遍历中再次切出B的左右子树，得到CD为B的左子树，右子树为空。

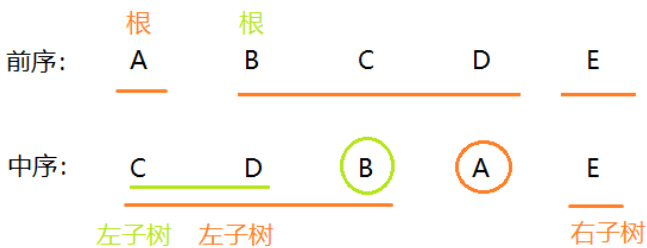
再以C为根节点，结合中序遍历，得到D为C的右子树，左子树为空。

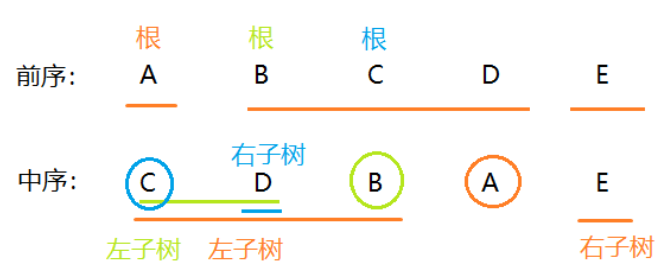
创建好的二叉树如下图所示：

     //使用先序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Pre_In(BinTreeNode<T> *&cur, const char *pre, const char *in, int n)
     {
         if (n <= )
         {
             cur = NULL;
             return;
         }
         int k = ;
         while (pre[] != in[k]) //再中序中找到pre[0]的值
         {
             k++;
         }
         cur = new BinTreeNode<T>(in[k]); //创建结点
         CreateBinTreeBy_Pre_In(cur->leftChild, pre + , in, k);
         CreateBinTreeBy_Pre_In(cur->rightChild, pre + k + , in + k + , n - k - );
     }

4.根据已知的后续遍历和中序遍历创建二叉树

根据后序遍历，先找到这棵树的根节点的值，也就是数组中最后一个节点(数组长度-1)的位置，由此创建根节点。
        然后在中序遍历中找到根的值所在的下标，切出左右子树的后续和中序。
        注意：如果后序遍历的数组长度为0，说明是一棵空树。

举例：

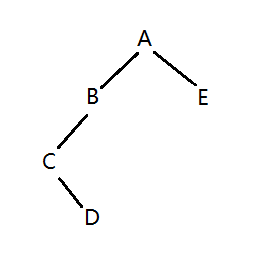
由后序遍历可以确定A是这棵树的根节点，然后根据中序遍历切出A的左右子树，得到CDB属于A的左子树，E属于A的右子树，如下图：

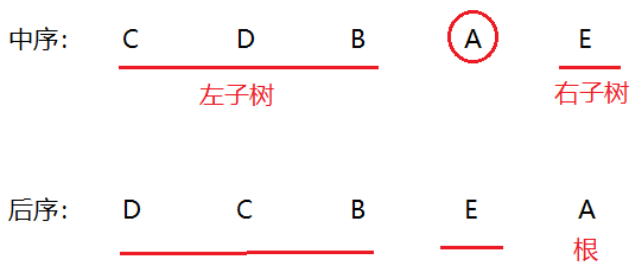
接着以B为根节点，在中序遍历中再次切出B的左右子树，得到CD为B的左子树，右子树为空。

再以C为根节点，结合中序遍历，得到D为C的右子树，左子树为空。

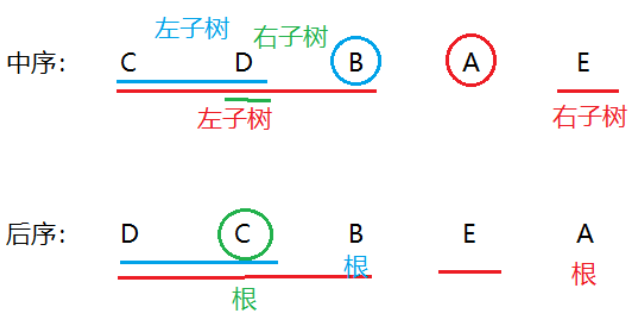
创建好的二叉树如下图所示：

 //使用后序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Post_In(BinTreeNode<T> *&cur, const char *post, const char *in, int n)
     {
         if (n == )
         {
             cur = NULL;
             return;
         }

         char r = *(post + n - );    //根结点值
         cur = new BinTreeNode<T>(r); //构造当前结点

         int k = ;
         const char *p = in;
         while (*p != r)
         {
             k++;
             p++;
         }
         CreateBinTreeBy_Post_In(cur->leftChild, post, in, k);
         CreateBinTreeBy_Post_In(cur->rightChild, post + k, p + , n - k - );
     }

二叉树的递归遍历

　　先序遍历：根->左->右

     //二叉树的先序遍历
     void PreOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             cout << subTree->data << " ";
             PreOrder(subTree->leftChild);
             PreOrder(subTree->rightChild);
         }
     }

　　中序遍历：左->根->右

     //二叉树的中序遍历
     void InOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             InOrder(subTree->leftChild);
             cout << subTree->data << " ";
             InOrder(subTree->rightChild);
         }
     }

　　后续遍历：左->右->根

     //二叉树的后序遍历
     void PostOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             PostOrder(subTree->leftChild);
             PostOrder(subTree->rightChild);
             cout << subTree->data << " ";
         }
     }

二叉树的非递归遍历

　　先序遍历

　　为了把一个递归过程改为非递归过程，一般需要利用一个工作栈，记录遍历时的回退路径。

 

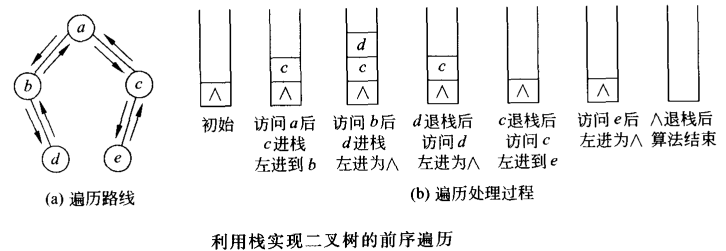
　　利用栈实现前序遍历的过程。每次访问一个结点后，在向左子树遍历下去之前，利用这个栈记录该结点的右子女（如果有的话）结点的地址，以便在左子树退回时可以直接从栈顶取得右子树的根结点，继续其右子树的前序遍历。

     //二叉树先序遍历(非递归1)
     void PreOrder_NoRecurve1(BinTreeNode<T> *p)
     {
         stack<BinTreeNode<T>*> S;
         S.push(NULL);    //最先push一个NULL，到最后一个结点没有左右子树时，栈里只有一个NULL了，令指针p指向这个NULL，再判断就会结束循环
         while (p!=NULL)
         {
             cout << p->data << " ";
             if(p->rightChild!=NULL)    //预留右子树指针在栈中
             {
                 S.push(p->rightChild);
             }

             if (p->leftChild!=NULL)    //进左子树
             {
                 p = p->leftChild;
             }
             else    //左子树为空
             {
                 p = S.top();
                 S.pop();
             }
         }
     }

另一种前序遍历的方法。为了保证先左子树后右子树的顺序，在进栈时是先进右子女结点地址，后进左子女结点地址，出栈时正好相反。

     //二叉树先序遍历（非递归2）
     void PreOrder_NoRecurve2(BinTreeNode<T> *p)
     {
         stack<BinTreeNode<T>*> S;
         BinTreeNode<T>* t;
         S.push(p);    //根节点进栈
         while (!S.empty())    //当栈不为空
         {
             t = S.top();    //p先记住栈顶元素，然后栈顶出栈
             S.pop();
             cout << t->data << " ";    //访问元素
             if (t->rightChild != NULL)    //右孩子不为空，右孩子近栈
             {
                 S.push(t->rightChild);
             }
             if (t->leftChild != NULL)    //左孩子不为空，左孩子进栈
             {
                 S.push(t->leftChild);
             }
         }
     }

　　中序遍历

　　需要使用一个栈，以记录遍历过程中回退的路径。在一棵子树中首先访问的是中序下的第一个结点，它位于从根开始沿leftChild链走到最左下角的结点，该结点的leftChild指针为NULL。访问它的数据之后，再遍历该结点的右子树。此右子树又是二叉树，重复执行上面的过程，直到该子树遍历完。

 

　　如果某结点的右子树遍历完或右子树为空，说明以这个结点为根的二叉树遍历完，此时从栈中退出更上层的结点并访问它，再向它的右子树遍历下去。

     //二叉树的中序遍历(非递归)
     void InOrder_NoRecurve(BinTreeNode<T>* p)
     {
         stack<BinTreeNode<T>*> S;
         do
         {
             while (p!=NULL)
             {
                 S.push(p);
                 p = p->leftChild;
             }
             if (!S.empty())
             {
                 p = S.top();
                 S.pop();
                 cout << p->data << " ";
                 p = p->rightChild;
             }
         }
         while (p!=NULL||!S.empty());
     }

　　后续遍历

思想：

1、如果栈顶元素非空且左节点存在,将其压入栈中，如果栈顶元素存在左节点，将其左节点压栈，重复该过程。直到左结点不存在则进入第2步
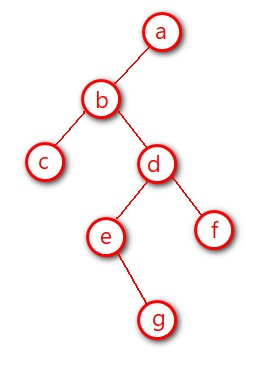
2、判断上一次出栈节点是否是当前栈顶结点的右节点(就是右叶子结点，如：g，f结点)，或者当前栈顶结点不存在右结点(如：g，f，a结点)，将当前节点输出，并出栈。否则将当前栈顶结点右孩子节点压栈，再进入第1步

     //后序遍历(非递归)
     void PostOrder_NoRecurve(BinTreeNode<T> *p)
     {
         if (root == NULL)
             return;
         stack<BinTreeNode<T> *> s;
         s.push(p);
         BinTreeNode<T> *lastPop = NULL;
         while (!s.empty())
         {
             while (s.top()->leftChild != NULL)
                 s.push(s.top()->leftChild);
             while (!s.empty())
             {
                 //右叶子结点 || 没有右结点
                 if (lastPop == s.top()->rightChild || s.top()->rightChild == NULL)
                 {
                     cout << s.top()->data << " ";
                     lastPop = s.top();
                     s.pop();
                 }
                 else if (s.top()->rightChild != NULL)
                 {
                     s.push(s.top()->rightChild);
                     break;
                 }
             }
         }
     }

　　层次遍历

    按层次顺序访问二叉树的处理需要利用一个队列。在访问二又树的某一层结点时，把下一层结点指针预先记忆在队列中，利用队列安排逐层访问的次序。因此，每当访问一个结点时，将它的子女依次加到队列的队尾，然后再访问已在队列队头的结点。这样可以实现二又树结点的按层访问。

 

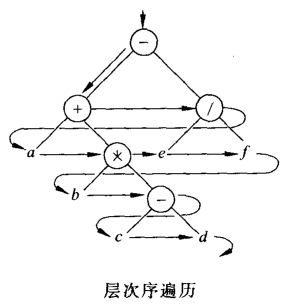
     //二叉树的层次遍历(非递归遍历)
     void LevelOrder(BinTreeNode<T> *p)
     {
         queue<BinTreeNode<T>*> Q;
         Q.push(p);    //根节点进队
         BinTreeNode<T>* t;
         while (!Q.empty())
         {
             t = Q.front();    //t先记住队头,再将队头出队
             Q.pop();
             cout << t->data << " ";    //访问队头元素的数据

             if (t->leftChild != NULL)
             {
                 Q.push(t->leftChild);
             }

             if (t->rightChild != NULL)
             {
                 Q.push(t->rightChild);
             }
         }
     }

二叉树的结点个数

     //计算二叉树以subTree为根的结点的个数
     int Size(BinTreeNode<T> *subTree) const
     {
         if (subTree == NULL)    //递归结束，空树结点个数为0
         {
             return ;
         }
         return  + Size(subTree->leftChild) + Size(subTree->rightChild);
     }

二叉树的高度

     //计算二叉数以subTree为根的高度
     int Height(BinTreeNode<T> *subTree)
     {
         if (subTree == NULL)    //递归结束，空树高度为0
         {
             return ;
         }
         int i = Height(subTree->leftChild);
         int j = Height(subTree->rightChild);
         return i < j ? j +  : i + ;
     }

以广义表的形式输出二叉树

     void PrintBinTree(BinTreeNode<T> *BT)
     {
         if (BT != NULL)    //树为空时结束递归
         {
             cout << BT->data;
             if (BT->leftChild != NULL || BT->rightChild != NULL)
             {
                 cout << '(';
                 if (BT->leftChild!=NULL)
                 {
                     PrintBinTree(BT->leftChild);
                 }
                 cout << ',';
                 if (BT->rightChild != NULL)
                 {
                     PrintBinTree(BT->rightChild);
                 }
                 cout << ')';
             }
         }
     }

求二叉树某结点的父节点

     //从结点subTree开始，搜索结点current的父节点,找到返回父节点的地址，找不到返回NULL
     BinTreeNode<T>* Parent(BinTreeNode<T>* subTree, BinTreeNode<T>* current)
     {
         if (subTree == NULL)
         {
             return NULL;
         }
         if (subTree->leftChild == current || subTree->rightChild == current)    //如果找到，返回父节点subTree
         {
             return subTree;
         }
         BinTreeNode<T>* p;
         if (p = Parent(subTree->leftChild, current) != NULL)    //递归在左子树中搜索
         {
             return p;
         }
         else
         {
             return Parent(subTree->rightChild, current);    //递归右子树中搜索
         }
     }

二叉树的销毁

     //二叉树的销毁函数
     void Destroy(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             Destroy(subTree->leftChild);
             Destroy(subTree->rightChild);
             delete subTree;
             subTree = NULL;
         }
     }

判断两颗二叉树是否相等

     //判断两颗二叉树是否相等
     bool equal(BinTreeNode<T> *a, BinTreeNode<T> *b)
     {
         if (a == NULL&&b == NULL)    //两者都为空
         {
             return true;
         }
         if (a != NULL&&b != NULL&&a->data == b->data&&equal(a->leftChild, b->leftChild) && equal(a->rightChild, b->rightChild))    //两者都不为空，且两者的结点数据相等，且两者的左右子树的结点都相等
         {
             return true;
         }
         return false;
     }

 完整代码：

 

 //结点类型
 template <typename T>
 struct BinTreeNode
 {
     T data;                                                                                                        //结点中存储的数据
     BinTreeNode<T> *leftChild, *rightChild;                                                                        //左子树和右子树
     BinTreeNode() : leftChild(NULL), rightChild(NULL) {}                                                           //无参构造函数
     BinTreeNode(T x, BinTreeNode<T> *l = NULL, BinTreeNode<T> *r = NULL) : data(x), leftChild(l), rightChild(r) {} //带默认值的有参构造参数
 };

 //二叉树类
 template <typename T>
 class BinaryTree
 {
 public:

 //==========二叉树构造与析构==========//

     //构造函数
     BinaryTree() : root(NULL) {}

     //指定结束标志的构造函数
     BinaryTree(T value) : RefValue(value), root(NULL) {}

     //析构函数
     ~BinaryTree() { Destroy(root); }

 //==========二叉树的创建==========//

     //使用广义表创建二叉树，以'#'字符代表结束
     void CreateBinTree() { CreateBinTree(root); }

     //前序遍历创建二叉树(前序遍历的应用)，用#表示空结点
     void CreateBinTree_PreOrder() { CreateBinTree_PreOrder(root); }

     //使用先序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Pre_In(const char *pre, const char *in)
     {
         int n = strlen(pre);
         CreateBinTreeBy_Pre_In(root, pre, in, n);
     }

     //使用后序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Post_In(const char *post, const char *in)
     {
         int n = strlen(post);
         CreateBinTreeBy_Post_In(root, post, in, n);
     }

 //==========二叉树的遍历==========//

     //先序遍历（递归）
     void PreOrder() { PreOrder(root); }

     //中序遍历(递归)
     void InOrder() { InOrder(root); }

     //后序遍历（递归）
     void PostOrder() { PostOrder(root); }

     //先序遍历(非递归)
     void PreOrder_NoRecurve() { PreOrder_NoRecurve(root); }

     //中序遍历(非递归)
     void InOrder_NoRecurve() { InOrder_NoRecurve(root); }

     //后序遍历(非递归)
     void PostOrder_NoRecurve() { PostOrder_NoRecurve(root); }

     //层次遍历(非递归)
     void LevelOrder() { LevelOrder(root); }

 //==========获取结点==========//

     //获取二叉树的根节点
     BinTreeNode<T> *getRoot() const
     {
         return root;
     }

     //获取current结点的父节点
     BinTreeNode<T> *Parent(BinTreeNode<T> *current)
     {
         return (root == NULL || root == current) ? NULL : Parent(root, current); //如果没有根节点或current结点就是root结点，就没有父节点
     }

     //获取current结点的左结点
     BinTreeNode<T> *LeftChild(BinTreeNode<T> *current)
     {
         return (current != NULL) ? current->leftChild : NULL;
     }

     //获取current结点的右结点
     BinTreeNode<T> *RightChild(BinTreeNode<T> *current)
     {
         return (current != NULL) ? current->rightChild : NULL;
     }

 //==========成员函数==========//

     //销毁函数
     void Destroy() { Destroy(root); }

     //拷贝二叉树(前序遍历的应用)
     BinaryTree(BinaryTree<T> &s)
     {
         root = Copy(s.getRoot());
     }

     //判断两颗二叉树是否相等(前序遍历的应用)
     bool operator==(BinaryTree<T> &s)
     {
         return (equal(this->getRoot(), s.getRoot()));
     }

     //计算二叉树的结点的个数(后序遍历的应用)
     int Size() { return Size(root); }

     //计算二叉树的高度（后序遍历的应用）
     int Height() { return Height(root); }

     //判断二叉树是否为空
     bool Empty() { return (root == NULL) ? true : false; }

     //以广义表的形式输出二叉树(前序遍历的应用)
     void PrintBinTree() { PrintBinTree(root); }

 protected:

     //使用广义表创建二叉树函数,这里以“字符”创建二叉树,以'#'字符代表结束
     void CreateBinTree(BinTreeNode<T> *&BT)
     {
         stack<BinTreeNode<T> *> s;
         BT = NULL;
         BinTreeNode<T> *p, *t; //p用来记住当前创建的节点，t用来记住栈顶的元素
         int k;                 //k是处理左、右子树的标记
         T ch;
         cin >> ch;

         while (ch != RefValue)
         {
             switch (ch)
             {
             case '(': //对(做处理
                 s.push(p);
                 k = ;
                 break;

             case ')': //对)做处理
                 s.pop();
                 break;

             case ',': //对,做处理
                 k = ;
                 break;

             default:
                 p = new BinTreeNode<T>(ch); //构造一个结点
                 if (BT == NULL)             //如果头节点是空
                 {
                     BT = p;
                 }
                 else if (k == ) //链入*t的左孩子
                 {
                     t = s.top();
                     t->leftChild = p;
                 }
                 else //链入*t的右孩子
                 {
                     t = s.top();
                     t->rightChild = p;
                 }
             }
             cin >> ch;
         }
     }

     //创建二叉树(利用已知的二叉树的前序遍历创建)用#表示空结点
     void CreateBinTree_PreOrder(BinTreeNode<T> *&subTree)
     {
         T item;
         if (cin >> item)
         {
             if (item != RefValue)
             {
                 subTree = new BinTreeNode<T>(item); //构造结点
                 if (subTree == NULL)
                 {
                     cout << "空间分配错误！" << endl;
                     exit();
                 }
                 CreateBinTree_PreOrder(subTree->leftChild);  //递归创建左子树
                 CreateBinTree_PreOrder(subTree->rightChild); //递归创建右子树
             }
             else
             {
                 subTree == NULL;
             }
         }
     }

     //使用先序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Pre_In(BinTreeNode<T> *&cur, const char *pre, const char *in, int n)
     {
         if (n <= )
         {
             cur = NULL;
             return;
         }
         int k = ;
         while (pre[] != in[k]) //再中序中找到pre[0]的值
         {
             k++;
         }
         cur = new BinTreeNode<T>(in[k]); //创建结点
         CreateBinTreeBy_Pre_In(cur->leftChild, pre + , in, k);
         CreateBinTreeBy_Pre_In(cur->rightChild, pre + k + , in + k + , n - k - );
     }
     //使用后序遍历和中序遍历创建二叉树
     void CreateBinTreeBy_Post_In(BinTreeNode<T> *&cur, const char *post, const char *in, int n)
     {
         if (n == )
         {
             cur = NULL;
             return;
         }

         char r = *(post + n - );    //根结点值
         cur = new BinTreeNode<T>(r); //构造当前结点

         int k = ;
         const char *p = in;
         while (*p != r)
         {
             k++;
             p++;
         }
         CreateBinTreeBy_Post_In(cur->leftChild, post, in, k);
         CreateBinTreeBy_Post_In(cur->rightChild, post + k, p + , n - k - );
     }

     //先序遍历(递归)
     void PreOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             cout << subTree->data << " ";
             PreOrder(subTree->leftChild);
             PreOrder(subTree->rightChild);
         }
     }

     //中序遍历(递归)
     void InOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             InOrder(subTree->leftChild);
             cout << subTree->data << " ";
             InOrder(subTree->rightChild);
         }
     }

     //后序遍历(递归)
     void PostOrder(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             PostOrder(subTree->leftChild);
             PostOrder(subTree->rightChild);
             cout << subTree->data << " ";
         }
     }

     //先序遍历（非递归）
     void PreOrder_NoRecurve(BinTreeNode<T> *p)
     {
         stack<BinTreeNode<T> *> S;
         BinTreeNode<T> *t;
         S.push(p);         //根节点进栈
         while (!S.empty()) //当栈不为空
         {
             t = S.top(); //p先记住栈顶元素，然后栈顶出栈
             S.pop();
             cout << t->data << " ";    //访问元素
             if (t->rightChild != NULL) //右孩子不为空，右孩子近栈
             {
                 S.push(t->rightChild);
             }
             if (t->leftChild != NULL) //左孩子不为空，左孩子进栈
             {
                 S.push(t->leftChild);
             }
         }
     }

     //中序遍历(非递归)
     void InOrder_NoRecurve(BinTreeNode<T> *root)
     {
         if (root == NULL)
             return;
         stack<BinTreeNode<T> *> s;
         s.push(root);
         while (!s.empty())
         {
             while (s.top()->leftChild != NULL) //将左结点依次入栈
             {
                 s.push(s.top()->leftChild);
             }
             while (!s.empty())
             {
                 BinTreeNode<T> *cur = s.top();
                 cout << cur->data << " ";
                 s.pop();
                 if (cur->rightChild != NULL)
                 {
                     s.push(cur->rightChild);
                     break;
                 }
             }
         }
     }

     //后序遍历(非递归)
     void PostOrder_NoRecurve(BinTreeNode<T> *p)
     {
         if (root == NULL)
             return;
         stack<BinTreeNode<T> *> s;
         s.push(p);
         BinTreeNode<T> *lastPop = NULL;
         while (!s.empty())
         {
             while (s.top()->leftChild != NULL)
                 s.push(s.top()->leftChild);
             while (!s.empty())
             {
                 //右叶子结点 || 没有右结点
                 if (lastPop == s.top()->rightChild || s.top()->rightChild == NULL)
                 {
                     cout << s.top()->data << " ";
                     lastPop = s.top();
                     s.pop();
                 }
                 else if (s.top()->rightChild != NULL)
                 {
                     s.push(s.top()->rightChild);
                     break;
                 }
             }
         }
     }

     //层次遍历(非递归)
     void LevelOrder(BinTreeNode<T> *p)
     {
         queue<BinTreeNode<T> *> Q;
         Q.push(p); //根节点进队
         BinTreeNode<T> *t;
         while (!Q.empty())
         {
             t = Q.front(); //t先记住队头,再将队头出队
             Q.pop();
             cout << t->data << " "; //访问队头元素的数据

             if (t->leftChild != NULL)
             {
                 Q.push(t->leftChild);
             }

             if (t->rightChild != NULL)
             {
                 Q.push(t->rightChild);
             }
         }
     }

     //从结点subTree开始，搜索结点current的父节点,找到返回父节点的地址，找不到返回NULL
     BinTreeNode<T> *Parent(BinTreeNode<T> *subTree, BinTreeNode<T> *current)
     {
         if (subTree == NULL)
         {
             return NULL;
         }
         if (subTree->leftChild == current || subTree->rightChild == current) //如果找到，返回父节点subTree
         {
             return subTree;
         }
         BinTreeNode<T> *p;
         if (p = Parent(subTree->leftChild, current) != NULL) //递归在左子树中搜索
         {
             return p;
         }
         else
         {
             return Parent(subTree->rightChild, current); //递归右子树中搜索
         }
     }

     //二叉树的销毁
     void Destroy(BinTreeNode<T> *&subTree)
     {
         if (subTree != NULL)
         {
             Destroy(subTree->leftChild);
             Destroy(subTree->rightChild);
             delete subTree;
             subTree = NULL;
         }
     }

     //复制二叉树函数，返回一个指针，给出一个以originNode为根复制的二叉树的副本
     BinTreeNode<T> *Copy(BinTreeNode<T> *originNode)
     {
         if (originNode == NULL)
         {
             return NULL;
         }
         BinTreeNode<T> *temp = new BinTreeNode<T>; //创建根结点
         temp->data = originNode->data;
         temp->leftChild = Copy(originNode->leftChild);
         temp->rightChild = Copy(originNode->rightChild);
         return temp;
     }

     //判断两颗二叉树是否相等
     bool equal(BinTreeNode<T> *a, BinTreeNode<T> *b)
     {
         if (a == NULL && b == NULL) //两者都为空
         {
             return true;
         }
         if (a != NULL && b != NULL && a->data == b->data && equal(a->leftChild, b->leftChild) && equal(a->rightChild, b->rightChild)) //两者都不为空，且两者的结点数据相等，且两者的左右子树的结点都相等
         {
             return true;
         }
         return false;
     }

     //计算二叉树以subTree为根的结点的个数
     int Size(BinTreeNode<T> *subTree) const
     {
         if (subTree == NULL) //递归结束，空树结点个数为0
         {
             return ;
         }
         return  + Size(subTree->leftChild) + Size(subTree->rightChild);
     }

     //计算二叉数以subTree为根的高度
     int Height(BinTreeNode<T> *subTree)
     {
         if (subTree == NULL) //递归结束，空树高度为0
         {
             return ;
         }
         int i = Height(subTree->leftChild);
         int j = Height(subTree->rightChild);
         return i < j ? j +  : i + ;
     }

     //以广义表的形式输出二叉树
     void PrintBinTree(BinTreeNode<T> *BT)
     {
         if (BT != NULL) //树为空时结束递归
         {
             cout << BT->data;
             if (BT->leftChild != NULL || BT->rightChild != NULL)
             {
                 cout << '(';
                 if (BT->leftChild != NULL)
                 {
                     PrintBinTree(BT->leftChild);
                 }
                 cout << ',';
                 if (BT->rightChild != NULL)
                 {
                     PrintBinTree(BT->rightChild);
                 }
                 cout << ')';
             }
         }
     }

 private:
     BinTreeNode<T> *root; //根节点
     T RefValue;           //数据输入停止的标志，需要一个构造函数
 };