计算几何-poj2451-HPI

This article is made by Jason-Cow.
Welcome to reprint.
But please post the article's address.

题意，求半平面交，并且保证有解

poj2451

给张图边界（|x,y|<=1000,题目为1e4）

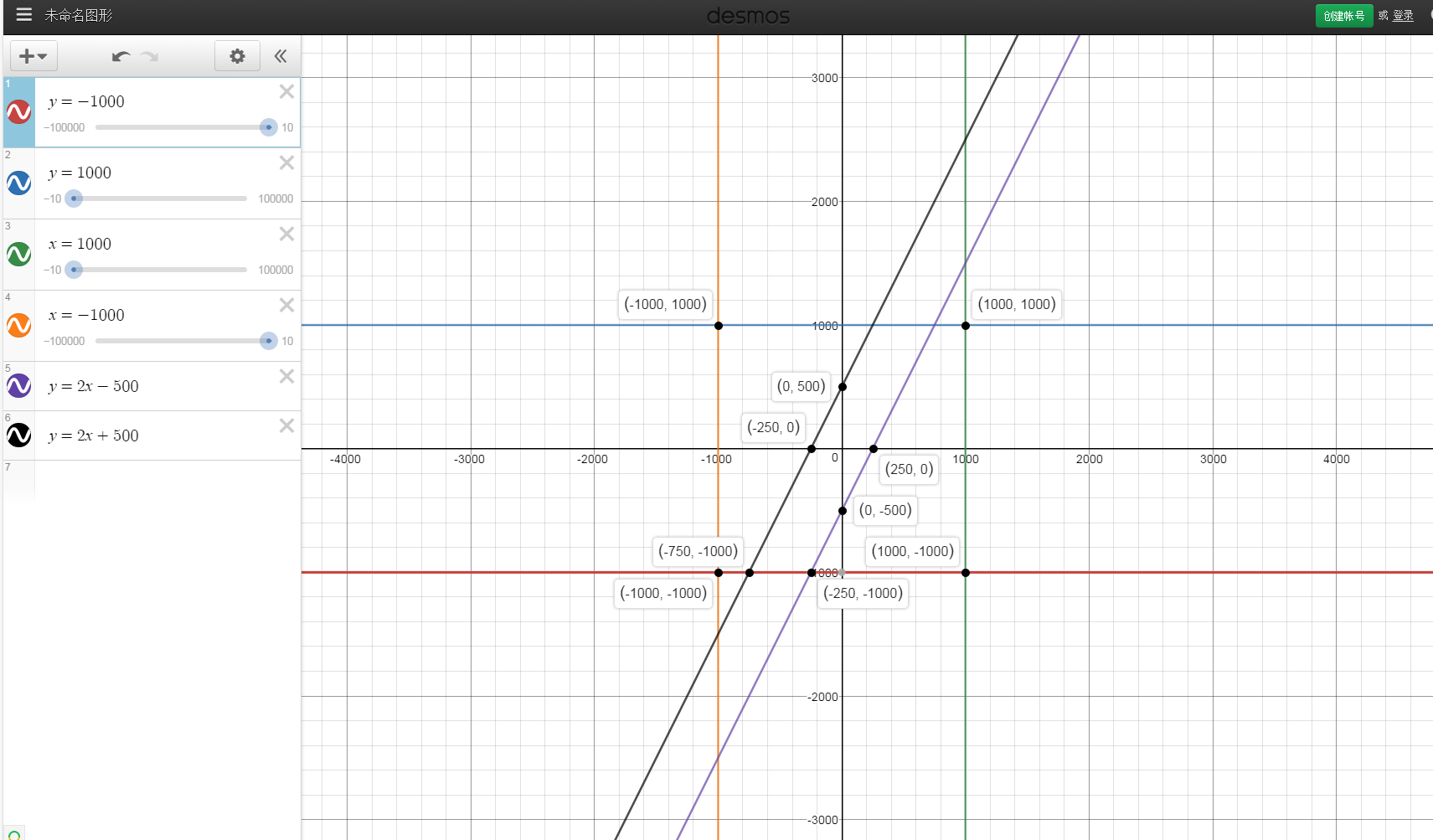
别问我为什么TLE

我当成多组处理没有判断文末符号，加上就！A！啦！

直接上模板

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <map>
 #include <set>
 using namespace std;
 #define sqr(x) ((x)*(x))
 #define RG register
 #define op operator
 #define IL inline
 typedef double db;
 typedef bool bl;
 const db pi=acos(-1.0),eps=1e-;
 struct D{
   db x,y;
   D(db x=0.0,db y=0.0):x(x),y(y){}
 };
 typedef D V;
 bl operator<(D A,D B){return A.x<B.x||(A.x==B.x&&A.y<B.y);}
 V operator+(V A,V B){return V(A.x+B.x,A.y+B.y);}
 V operator-(V A,V B){return V(A.x-B.x,A.y-B.y);}
 V operator*(V A,db N){return V(A.x*N,A.y*N);}
 V operator/(V A,db N){return V(A.x/N,A.y/N);}

 db Ang(db x){return(x*180.0/pi);}
 db Rad(db x){return(x*pi/180.0);}
 V Rotate(V A,db a){return V(A.x*cos(a)-A.y*sin(a),A.x*sin(a)+A.y*cos(a));}
 db Dis(D A,D B){return sqrt(sqr(A.x-B.x)+sqr(A.y-B.y));}
 db Cross(V A,V B){return A.x*B.y-A.y*B.x;}

 db Area(D*R,int n){
     db S=0.0;
     for(int i=;i<n;i++)S+=Cross(R[i]-R[],R[i+]-R[]);
     return S/;
 }

 db Length(D*R,int n){
     db C=0.0;
     for(int i=;i<=n;i++)C+=Dis(R[i],R[i-]);
     return C+Dis(R[n],R[]);
 }

 struct L{
   D P,v;
   db a;
   L(){}
   L(D P,V v):P(P),v(v){a=atan2(v.y,v.x);}
   bool operator<(const L x)const{return a<x.a;}
 };

 D Intersect(L a,L b){
   V u=a.P-b.P;
   return a.P+a.v*(Cross(b.v,u)/Cross(a.v,b.v));
 }

 bool Left(L l,D A){
   return Cross(l.v,A-l.P)>;
 }

 int HPI(L*l,int n,D*ans){
   int head,tail,m=;
   D*P=new D[n];L*q=new L[n];
   sort(l+,l+n+),q[head=tail=]=l[];
   for(int i=;i<=n;i++){
     while(head<tail && !Left(l[i],P[tail-]))tail--;
     while(head<tail && !Left(l[i],P[head]))  head++;
     q[++tail]=l[i];
     if(fabs(Cross(q[tail].v,q[tail-].v))<eps){
       tail--;
       if(Left(q[tail],l[i].P))q[tail]=l[i];
     }
     if(head<tail)P[tail-]=Intersect(q[tail-],q[tail]);
   }
   while(head<tail && !Left(q[head],P[tail-]))tail--;
   if(tail-head<=)return ;
   P[tail]=Intersect(q[tail],q[head]);
   for(int i=head;i<=tail;i++)ans[++m]=P[i];
   return m;
 }

 const int maxn=2e4+;
 L l[maxn];D A[maxn];
 int main(){
   D LU(,1e4),LD(,),RD(1e4,),RU(1e4,1e4);
   for(int n;scanf("%d",&n)!=EOF;){
     for(int i=;i<=n;i++){
       db a,b,c,d;
       scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
       D A(a,b),B(c,d);
       l[i]=L(A,B-A);
     }
     l[++n]=L(LU,V(,-));
     l[++n]=L(LD,V(,));
     l[++n]=L(RD,V(,));
     l[++n]=L(RU,V(-,));
     int m=HPI(l,n,A);
     printf("%.1lf\n",Area(A,m));
   }
   return ;
 }