TopCoder SRM 566 Div 1 - Problem 1000 FencingPenguins

传送门：https://284914869.github.io/AEoj/566.html

题目简述：

平面上有中心在原点，一个点在(r,0)处的正n边形的n个顶点。
平面上还有m个企鹅，每个企鹅有一个位置和一个颜色，
现在要连一些边，使得每个点的度数都是0或2，
这样会构成若干个顶点不相交的圈，求满足以下条件的连边方案数：
1、每个圈里有至少一个企鹅；
2、任意两个圈不相交；
3、每种颜色的企鹅在同一个有限区域中；
4、每个企鹅在一个有限区域内；
n<=222,m<=50,r<=10^5, 
企鹅的颜色保证是大写字母或者小写字母，
坐标范围<=10^5,企鹅离任一条n个点连的边的距离>10^-6

思路：

很显然这题要用dp。考虑怎么用dp做。

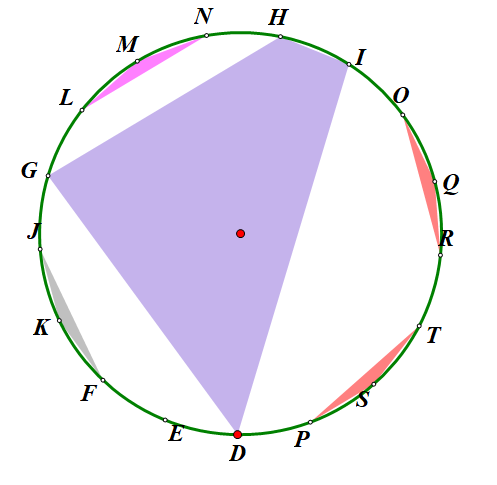
如图所示

我们先定义“特殊”多边形为有>=3条边的多边形或一个点。如图有6个多边形（包括点E）。

这样所有的点就都在多边形上了。

我们选任意一个点作为起点。例如D。

D所在的多边形为DGHI。这样弧DG,GH,HI,ID上的点形成的多边形就是互不干扰的了。

所以初步构思，可以从若干个小弧的状态推到一个大弧的状态。（我可能说不清楚具体过程，感性理解）

还有一个问题就是同颜色的企鹅在同一个多边形内。

这个限制可以转换为，所有的边两侧不存在同颜色的企鹅，且所有企鹅都不在多边形外部。

那么写起来就更方便了。

代码：

 #include <cmath>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 #define _CLASSNAME_ FencingPenguins
 #define _METHODNAME_ countWays
 #define _RC_ int
 #define _METHODPARMS_ int _n, int _r, vector<int> _x, vector<int> _y, string _c
 #define ref(i,x,y)for(int i=x;i<=y;++i)
 #define def(i,x,y)for(int i=x;i>=y;--i)
 #define reset(a)memset(a,0,sizeof a)
 const double pi=acos(-);
 const int mod=;
 struct point{
     double x,y;
     point(){x=;y=;}
     point(double X,double Y){x=X,y=Y;}
 };
 point operator -(point a,point b){ return point(a.x-b.x,a.y-b.y); }
 double operator ^(point a,point b){ return a.y*b.x-a.x*b.y; }
 int n,m,r,ans;
 int p_c[],fg[],sum[][];
 point O[],p[];
 bool ok[][];
 void inc(int&a,int b){a+=b;if(a>=mod)a-=mod;}
 int mul(int a,int b){return 1LL*a*b%mod;}
 int chd(char c){if(c>='a'&&c<='z')return c-'a';else return c-'A'+;}
 void work1(){
     reset(ok); reset(sum); ans=;
     ref(i,,n-) O[i]=point(r*cos(*pi*i/n),r*sin(*pi*i/n));
     ref(i,,n-)ok[i][i]=;
     ref(i,,n-)ref(j,i+,n-){
         ref(k,,)fg[k]=;
         ref(k,,m){
             int C=p_c[k]; double s=(O[j]-O[i])^(p[k]-O[i]);
             if(!fg[C])fg[C]=(s>)+;else if(fg[C]!=-) if(fg[C]!=(s>)+)fg[C]=-;
             sum[i][j]+=(s>);
         }
         bool flag=; ref(k,,)flag=flag&&(fg[k]>=);
         ok[i][j]=ok[j][i]=flag; sum[j][i]=m-sum[i][j];
     }
     ref(i,,n-)ref(j,,n-) sum[i+n][j]=sum[i][j+n]=sum[i+n][j+n]=sum[i][j];
     ref(i,,n-)ref(j,,n-) ok[i+n][j]=ok[i][j+n]=ok[i+n][j+n]=ok[i][j];
 }
 int dp1[][][],dp2[][]; bool tri[][][];
 void work2()
 {
     reset(dp1); reset(dp2); reset(tri);
     ref(i,,n-)if(sum[i][i+])return;
     ref(i,,n-)ref(j,i,i+n-)ref(k,i+,j-)tri[i][k][j]=(sum[i][j]-sum[i][k]-sum[k][j]>);
     ref(i,,n*-)dp1[i][i][]=,dp2[i][i]=;
     ref(len,,n-){
         ref(i,,n-){
             int j=i+len;
             ref(k,i,j-) if(!tri[i][k+][j]&&!tri[i][j][j+])
                 if(ok[k+][j])inc(dp2[i][j],mul(dp2[i][k],dp1[k+][j][]));
             inc(dp1[i][j][],dp2[i][j-]);
             ref(k,i+,j-)ref(d,,)
                 inc(dp1[i][j][d|tri[i][k][j]],mul(dp1[i][k][d],dp2[k][j-]));
             if(j<n)dp1[i+n][j+n][]=dp1[i][j][],dp1[i+n][j+n][]=dp1[i][j][];
             if(j<n)dp2[i+n][j+n]=dp2[i][j];
         }
     }
     if(!tri[n-][n][n+])ans=dp2[][n-];
     ref(i,,n-)if(ok[][i])inc(ans,mul(dp1[][i][],dp2[i][n-]));
 }
 class _CLASSNAME_{
 public:
     _RC_ _METHODNAME_(_METHODPARMS_)
     {
         n=_n; m=_x.size(); r=_r;
         ref(i,,m)p[i].x=_x[i-],p[i].y=_y[i-];
         ref(i,,m)p_c[i]=chd(_c[i-]);
         work1();work2();
         return _RC_(ans);
     }

 // BEGIN CUT HERE
     public:
     void run_test(int Case) { if ((Case == -) || (Case == )) test_case_0(); if ((Case == -) || (Case == )) test_case_1(); if ((Case == -) || (Case == )) test_case_2(); if ((Case == -) || (Case == )) test_case_3(); if ((Case == -) || (Case == )) test_case_4(); if ((Case == -) || (Case == )) test_case_5(); if ((Case == -) || (Case == )) test_case_6(); if ((Case == -) || (Case == )) test_case_7(); }
     private:
     //template <typename T> string print_array(const vector<T> &V) { ostringstream os; os << "{ "; for (typename vector<T>::const_iterator iter = V.begin(); iter != V.end(); ++iter) os << '\"' << *iter << "\","; os << " }"; return os.str(); }
     void verify_case(int Case, const int &Expected, const int &Received) { cerr << "Test Case #" << Case << "..."; if (Expected == Received) cerr << "PASSED" << endl; else { cerr << "FAILED" << endl; cerr << "\tExpected: \"" << Expected << '\"' << endl; cerr << "\tReceived: \"" << Received << '\"' << endl; } }
     void test_case_0() { int Arg0 = ; int Arg1 = ; int Arr2[] = {}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "R"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_1() { int Arg0 = ; int Arg1 = ; int Arr2[] = {,-}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {,-}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "RR"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_2() { int Arg0 = ; int Arg1 = ; int Arr2[] = {,-,-,}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {,-,,-}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "BBBB"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_3() { int Arg0 = ; int Arg1 = ; int Arr2[] = {,-,-,}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {,-,,-}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "RGBY"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_4() { int Arg0 = ; int Arg1 = ; int Arr2[] = {,}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {-,}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "rB"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_5() { int Arg0 = ; int Arg1 = ; int Arr2[] = {}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "y"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_6() { int Arg0 = ; int Arg1 = ; int Arr2[] = {,,,,-,-,,-,}; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {-,,,,,,,-,-}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "YBYBWWBRr"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
     void test_case_7() { int Arg0 = ; int Arg1 = ; int Arr2[] = {, , , , , , , , , , , , , -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, , , , , , , , , , , , }; vector <int> Arg2(Arr2, Arr2 + (sizeof(Arr2) / sizeof(Arr2[]))); int Arr3[] = {, , , , , , , , , , , , , , , , , , , , , , , , , -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -, -}; vector <int> Arg3(Arr3, Arr3 + (sizeof(Arr3) / sizeof(Arr3[]))); string Arg4 = "xidylnzmnsolwfyhgjaegnwgazjbdmfwaldsmqxpowtianiesx"; int Arg5 = ; verify_case(, Arg5, countWays(Arg0, Arg1, Arg2, Arg3, Arg4)); }
 // END CUT HERE

 };
 // BEGIN CUT HERE
 int main()
 {
     _CLASSNAME_ user;
     user.run_test(-);
 }
 // END CUT HERE