●BZOJ 3529 [Sdoi2014]数表

题链：

http://www.lydsy.com/JudgeOnline/problem.php?id=3529

题解：

莫比乌斯反演。

按题目的意思，令$f(i)$表示i的所有约数的和，就是要求：

$ANS=\sum f(gcd(i,j))，满足1 \leq i \leq n，1 \leq j \leq m，且 f(gcd(i,j))\leq a$

---

首先 $f(i)$ 应该还是比较好推的，利用其为积性函数的特点，可以在线性筛时完成计算。

令$g[k]$表示$gcd(i,j)=k$的$(i,j)$的对数

$G[k]$表示$gcd(i,j)=\lambda k$的$(i,j)$的对数，其值$G[k]=\lfloor \frac{n}{k} \rfloor \lfloor \frac{m}{k} \rfloor$

那么显然，$G[k]$为$g[k]$的倍数关系和函数，

即满足$G[k]=\sum_{k|d} g[d]$

则由莫比乌斯反演得：

$g[k]=\sum_{k|d}\mu(\frac{d}{k})G[d]$

$\quad\quad=\sum_{k|d}\mu(\frac{d}{k})\lfloor \frac{n}{d} \rfloor \lfloor \frac{m}{d} \rfloor$

那么现在，直接从gcd的值的角度出发，ANS可以写成如下形式：

$ANS=\sum_{i=1}^{min(n,m)}f(i)g(i)$

$\quad\quad=\sum_{i=1}^{min(n,m)}f(i)\sum_{i|d}\mu(\frac{d}{i})\lfloor \frac{n}{d} \rfloor \lfloor \frac{m}{d} \rfloor$

然后再化一下：

$\quad\quad=\sum_{d=1}^{min(n,m)}\lfloor \frac{n}{d} \rfloor \lfloor \frac{m}{d} \rfloor\sum_{i|d}f(i)\mu(\frac{d}{i})$

令 $w(d)=\sum_{i|d}f(i)\mu(\frac{d}{i})$

那么$ANS=\sum_{d=1}^{min(n,m)}\lfloor \frac{n}{d} \rfloor \lfloor \frac{m}{d} \rfloor w(d)$

如果不考虑题目中$f(gcd(i,j))\leq a$的限制

我们就可以枚举每个i，然后把其倍数$d=\lambda i$的$w(d)+=f(i)\mu(\frac{d}{i})$

以此计算出所有的w(d)，复杂度为O(Nlog_2N)的。

然后那个求ANS的式子就可以运用向下取整的特性进行分块计算，就可以达到每个询问$O(\sqrt N)$的复杂度。

再来考虑有a的限制时的做法，（其实也不麻烦）

离线询问，按a从小到大排序，

同时把f(i)按从小到大排序，

一次遍历每个询问，并把$f(i)$小于当前询问的$a$的$i$按之前的做法：枚举倍数，加入对应的$w(d)$。

但是为了维护好前缀和，以便使用分块计算，

所以用树状数组维护，即把值$f(i)\mu(\frac{d}{i})$加入到树状数组里面。

然后同样的用树状数组查询前缀和就可以继续对当前询问进行分块计算了。

复杂度：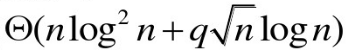

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 100050
using namespace std;
struct BIT{
	int val[MAXN],N;
	void Reset(int n){memset(val,0,sizeof(val));N=n;}
	int Lowbit(int p){return p&-p;}
	void Modify(int p,int v){
		while(p<=N) val[p]+=v,p+=Lowbit(p);
	}
	int Query(int p,int ret=0){
		while(p) ret+=val[p],p-=Lowbit(p);
		return ret;
	}
}DT;
struct Question{
	int n,m,a,id;
	friend bool operator < (Question A,Question B){
		return A.a<B.a;
	}
}Q[MAXN];
int f[MAXN],fi[MAXN],mu[MAXN],ANS[MAXN];
bool cmp(int i,int j){
	return f[i]<f[j];
}
void Sieve(){
	static bool np[MAXN];
	static int prime[MAXN],pnt,tmp;
	mu[1]=f[1]=fi[1]=1;
	for(int i=2;i<=100000;i++){
		fi[i]=i;
		if(!np[i]) prime[++pnt]=i,mu[i]=-1,f[i]=1+i;
		for(int j=1;j<=pnt&&i<=100000/prime[j];j++){
			np[i*prime[j]]=1;
			if(i%prime[j]){
				mu[i*prime[j]]=-mu[i];
				f[i*prime[j]]=f[i]*f[prime[j]];
			}
			else{
				mu[i*prime[j]]=0;
				tmp=i; while(!(tmp%prime[j])) tmp=tmp/prime[j];
				f[i*prime[j]]=f[i]*prime[j]+f[tmp];
			}
			if(i%prime[j]==0) break;
		}
	}
	sort(fi+1,fi+100000+1,cmp);
}
int main(){
	Sieve(); int Case,ret,mini,n,m;
	scanf("%d",&Case);
	DT.Reset(100000);
	for(int i=1;i<=Case;i++)
		scanf("%d%d%d",&Q[i].n,&Q[i].m,&Q[i].a),Q[i].id=i;
	sort(Q+1,Q+Case+1);
	for(int q=1,p=1;q<=Case;q++){
		while(p<=100000&&f[fi[p]]<=Q[q].a){
			for(int d=fi[p];d<=100000;d+=fi[p])
				DT.Modify(d,f[fi[p]]*mu[d/fi[p]]);
			p++;
		}
		ret=0; n=Q[q].n; m=Q[q].m; mini=min(n,m);
		for(int i=1,last;i<=mini;i=last+1){
			last=min(n/(n/i),m/(m/i));
			ret+=(DT.Query(last)-DT.Query(i-1))*(n/i)*(m/i);
		}
		ANS[Q[q].id]=ret;
	}
	for(int i=1;i<=Case;i++)
		printf("%d\n",ANS[i]&(int)((1ll<<31)-1));
	return 0;
}