[BZOJ]1045 圆上的整点(HAOI2008)

　　数学题第二弹！

Description

　　求一个给定的圆(x^2+y^2=r^2)，在圆周上有多少个点的坐标是整数。

Input

　　一个正整数r。

Output

　　整点个数。

Sample Input

　　4

Sample Output

　　4

HINT

　　r<=2000 000 000

Solution

　　小C不想写题解啊啊啊啊！！！！

　　题解在这里啊啊啊啊！！！！（看完记得投币！！！！）

　　我爱数学啊啊啊啊！！！！

　　开玩笑的，还是说一说题解吧。

　　相信如果你认真看完了上面那个视频的前25min，心里肯定已经有不下一万种解法了。

　　小C先口胡两句，你们意会就好。

　　　　题目要我们求的是以原点为圆心，半径为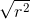的圆经过了多少个整点。

　　　　所以我们只要把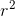的所有因数的函数值相加的和乘上4就是答案。

　　请完全无视上面两行！完全无视！现在说正经的：

　　根据我们的知识储备，我们知道，对于圆。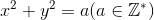

　　将a进行质因数分解，得。

　　如果存在i使得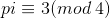且为奇数，那么该圆不经过任何整点。

　　否则答案就是。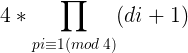

　　根据上面的结论，由于题目中的a是完全平方数，所以不存在di为奇数的情况，因此必定经过整点。

　　所以我们只要把r质因数分解，挑出其中形如4k+1的质数，该质数的指数为d，对答案的贡献就是乘上2*d+1。

　　时间复杂度是质因数分解的。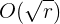

#include <cstdio>
#include <algorithm>
#include <cstring>
#define MN 60005
using namespace std;
int n,ans,pin,pri[MN];
bool u[MN];

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

int main()
{
    register int i,j,lt;
    n=read(); ans=;
    for (i=;1LL*i*i<=n;++i)
    {
        if (!u[i]) pri[++pin]=i;
        for (j=;1LL*i*i*pri[j]*pri[j]<=n;++j)
        {
            u[i*pri[j]]=true;
            if (i%pri[j]==) break;
        }
    }
    while (n%pri[]==) n/=pri[];
    for (i=;i<=pin;++i)
    {
        for (lt=;n%pri[i]==;++lt) n/=pri[i];
        if (pri[i]%==) ans*=lt<<|;
    }
    if (n!=&&n%==) ans*=;
    printf("%d",ans<<);
}

Last Word

　　我在B站学数学.jpg

　　开什么玩笑！B站本来就是优秀的在线学习网站！（小C口胡不下去了）