洛谷P3268 [JLOI2016]圆的异或并（扫描线）

扫描线还不是很熟啊……不管是从想的方面还是代码实现的方面……

---

关于这题，考虑一条平行于\(y\)轴的扫描线从左到右扫描每一个圆，因为只有相离和内含两种关系，只用在切线处扫描即可

我们设上半圆为1，下半圆为-1，当前遍历到的圆为\(i\)。然后把每个圆弧按照和这条扫描线的交点的纵坐标从小到大排序，然后找每个下半圆的前驱，设这个前驱对应的圆为\(j\)。

如果这个前驱为上半圆，即这两个圆相离，状态相同

如果这个前驱为下半圆，即圆\(i\)内含于圆\(j\)，状态相反

嘛……不理解的话直接上图好了,紫圆为圆\(i\)，紫点为圆\(i\)的前驱，显然紫点对应的是个上半圆，状态相同

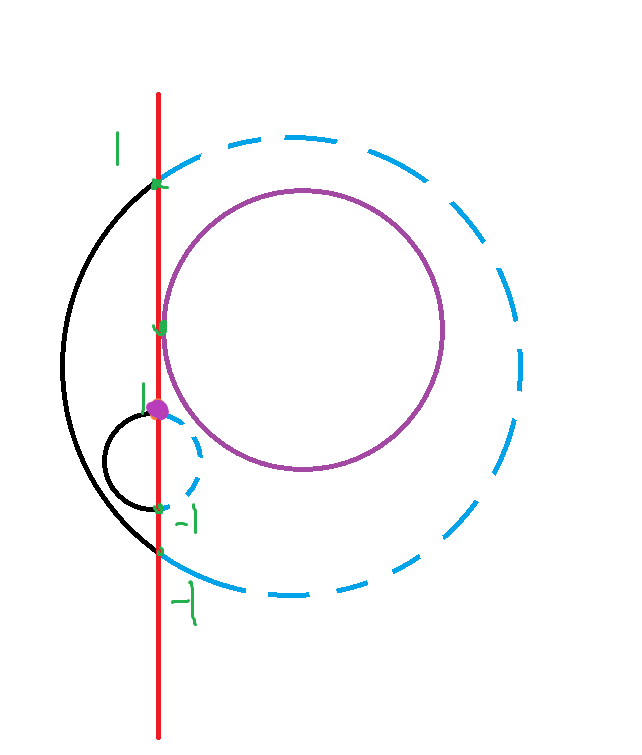
维护前驱可以用set维护，扫描到右切线时记得要删除半圆

代码

#include <bits/stdc++.h>
#define N 200010
#define ll long long
#define rep(i,x,y) for(i=(x);i<=(y);++i)
using namespace std;

const double eps=1e-9;
int x[N],y[N],r[N],nx,use[N];

struct point{
    int id,f;
    int X(){ return x[id]-f*r[id]; }
    friend bool operator <(point a,point b){ return (a.X()==b.X())?r[a.id]<r[b.id]:a.X()<b.X(); }
}p[N<<1];
struct pos{
    int id,f;
    double cycY(){
        double tmp=sqrt(1.0*r[id]*r[id]-1.0*(nx-x[id])*(nx-x[id]));
        return 1.0*y[id]+1.0*f*tmp;
    }
    friend bool operator <(pos a,pos b){ return (fabs(a.cycY()-b.cycY())<eps)?a.f<b.f:a.cycY()<b.cycY();  }
};
set<pos>qwq;
set<pos>::iterator it;

int main(){
    int n,i;
    ll ans=0;
    scanf("%d",&n);
    rep(i,1,n){
        scanf("%d%d%d",&x[i],&y[i],&r[i]);
        p[i]=(point){i,1},p[i+n]=(point){i,-1};
    }
    sort(p+1,p+2*n+1);
    rep(i,1,2*n){
        nx=p[i].X();
        if(p[i].f==1){
            it=(qwq.insert((pos){p[i].id,1})).first;
            if(it==qwq.begin()) use[p[i].id]=1;
            else{
                it--;
                if((*it).f==1) use[p[i].id]=use[(*it).id];
                else use[p[i].id]=-use[(*it).id];
            }
            qwq.insert((pos){p[i].id,-1});
        } else{
            qwq.erase((pos){p[i].id,1});
            qwq.erase((pos){p[i].id,-1});
        }
    }
    rep(i,1,n) ans+=1ll*use[i]*r[i]*r[i];
    printf("%lld\n",ans);
}