DP Training（Updating）♪(^∇^*)

DP Training

DP Training 01

https://vjudge.net/contest/220286 密码 nfls

A 数塔（Easy）

\(f[i][j]\) 表示当前选第 \(i\) 行，第 \(j\) 列的格子，上面的选完了，下面的没选的最大方案

\(f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]\)

B 数塔（Medium）

不难发现答案一定是交点到四个顶点的最大路径之和，预处理 \(f[4][i][j]\) 表示 \((i,j)\) 到四个定点的最优距离，然后枚举交点计算结果

注意有两种情况：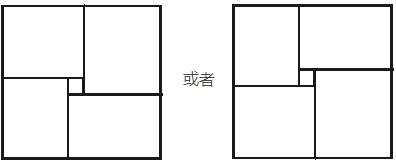

分别统计答案即可

C 数塔（Hard）

题目坏掉了

写了一个不知道真的假的

我们把来回想象成两个人一起从左上角走到右下角， \(f[i][j][k]\) 表示当前走到第 \(i\) 行，第一个人在第 \(j\) 列，第二个人在第 \(k\) 列，最大收益，转移的时候枚举第一个人是否是从左边来的，第二个人是否是从左边来的（否则就是从上边来的），复杂度 \(O(n^3)\)

D 最大连续和（Easy）

这个好像不用\(\text{dp}\)，直接维护一个当前的和以及当前的和对应的左端点

每次如果当前和>=0，那么就加上现在这个数，否则当前和改成现在这个数，左端点改成现在的位置（显然前面的负数没有意义）

rep(i,1,n){
	if(nw>=0 && nwl) nw+=a[i];
	else nwl=i,nw=a[i];
   if(nw>ans){ans=nw;ansl=nwl;ansr=i;}
}

E 最大连续和（Medium）

跟D一样的做法

首先枚举左边界和右边界，然后就把二维问题转化成了一维问题，每一个数就是对应的行的左边界与右边界之间数的和，然后用上面的方法求一下最大连续和即可，复杂度 \(O(n^3)\)

F 最大连续和（Hard）

垃圾题目

一眼看上去不可做，网上翻一下题解，复杂度 \(O(nm)\) ？题目中根本没有说明 \(m\) 的范围，我以为 \(m\) 可以达到\(1\text{e}6\)……

然后就好做了，想怎么做怎么做

先记一个 \(f[i][j]\) 表示当前选到第 \(i\) 个数，当前选了 \(j\) 段，最大的收益

转移就是

\[f[i][j]=MAX(f[i-1][j],MAX_{0 \le k \lt i}{f[k][j-1]})+a[i]
\]

然后记录一个前缀MAX就可以做到 \(O(nm)\) 了，注意空间需要滚动数组优化

G 最长上升子序列（Easy）

\(O(n^2)\) 暴力dp。。。

H 最长上升子序列（Medium1）

可以证明答案就是LIS的长度

不过我用的是贪心的做法，维护一个set存储每一个拦截系统的上一个高度，每次把当前导弹赋给大于等于他的最小的那个，如果不存在，则新建一个导弹拦截系统。容易证明正确性。

注意多测。。。

I 最长上升子序列（Medium2）

把第一维排序，第二维跟着变换，求变换后的LIS

注意输出的时候road和roads不一样，而且king的首字母小写，两个test之间有一个换行。。。

J 最长公共子序列（Easy）

为什么HDU的题这么多都没有数据范围啊。。。

直接写显然是 \(O(nm)\) 的，然后把数组开到 \(5000 \times 5000\)，就过了。。。

K 最长公共子序列（Medium）

跟上一题基本一样，不过有数据范围（