算法复习——数位dp

开头由于不知道讲啥依然搬讲义

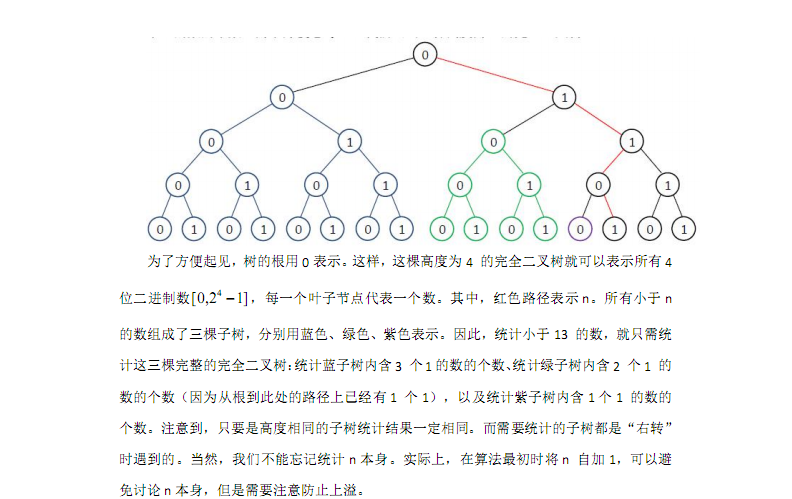
对于引入的这个问题,讲义里已经很清楚了,我更喜欢用那个建树的理解····

相当于先预处理f,然后从起点开始在树上走··记录目前已经找到了多少个满足题意的数k,如果枚举到第i位,下一位要走的是1，需要加上左子树的总数f[i-1][K-k],如果下一位走的是0直接走左子树即可····

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int f[N][N],x,y,k,b,num[N],n,ans1,ans2;
inline void pre()
{
  for(int i=;i<=;i++)
  {
    f[i][]=f[i][i]=;
    for(int j=;j<i;j++)
      f[i][j]=f[i-][j]+f[i-][j-];
  }
}
inline void trans(int x)
{
  int temp=x;n=;
  while(temp)  num[++n]=temp%b,temp/=b;
}
inline int solve()
{
  int tot=,sum=,i;
  for(i=n;i>=;i--)
  {
    if(num[i]>)   //大于1的话此时整个子树代表的数都是小于x的，因此直接统计答案
    {
      sum+=f[i][k-tot];  break;
    }
    else if(num[i]==)
    {
      sum+=f[i-][k-tot];   //等于1统计左儿子的答案（即小于该数且又有k个1的数的个数）
      if(++tot>k)  break;
    }
  }
  if(i!=&&tot==k)  sum++;  //如果该数本身就符合答案的话答案加1
  return sum;
}
int main()
{
  //freopen("a.in","r",stdin);
  pre();
  scanf("%d%d%d%d",&x,&y,&k,&b);
  trans(y),ans1=solve();
  trans(x-),ans2=solve();
  cout<<ans1-ans2<<endl;
  return ;
}

例题：

1.windy数（bzoj1026）

Description

　　windy定义了一种windy数。不含前导零且相邻两个数字之差至少为2的正整数被称为windy数。 windy想知道，
在A和B之间，包括A和B，总共有多少个windy数？

Input

　　包含两个整数，A B。

Output

　　一个整数

Sample Input

【输入样例一】
1 10
【输入样例二】
25 50

Sample Output

【输出样例一】
9
【输出样例二】
20

HINT

【数据规模和约定】

100%的数据，满足 1 <= A <= B <= 2000000000 。

Source

首先运用数位dp的常规思想，用ans(B)-ans(A-1);

这道题我们用f[i][j][0/1]表示第j位为i且小于/大于原数前i为满足题意的数的个数,然后枚举上一位进行dp即可·····具体看代码··

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int f[N][N][],num[N],n,a,b;
inline int Abs(int a)
{
  return a<?-a:a;
}
inline int solve(int x)
{
  if(!x)  return ;
  n=;memset(f,,sizeof(f));int ans=;
  while(x)  num[++n]=x%,x/=;
  for(int i=;i<=;i++)
    if(i<=num[])  f[i][][]=;
    else f[i][][]=;
  for(int i=;i<=n;i++)
    for(int j=;j<=;j++)
      for(int k=;k<=;k++)
        if(Abs(j-k)>=)
        {
          if(j<num[i])  f[j][i][]+=f[k][i-][]+f[k][i-][];
          else if(j==num[i])  f[j][i][]+=f[k][i-][],f[j][i][]+=f[k][i-][];
          else f[j][i][]+=f[k][i-][]+f[k][i-][];
        }
  for(int i=;i<=;i++)
  {
    ans+=f[i][n][];
    if(i==num[n])  break;
  }
  for(int i=n-;i>=;i--)
    for(int j=;j<=;j++)
      ans+=f[j][i][]+f[j][i][];
  return ans;
}
int main()
{
  //freopen("a.in","r",stdin);
  scanf("%d%d",&a,&b);
  printf("%d\n",solve(b)-solve(a-));
  return ;
}

2.不要62（hdu2089）

Problem Description

杭州人称那些傻乎乎粘嗒嗒的人为62（音：laoer）。
杭州交通管理局经常会扩充一些的士车牌照，新近出来一个好消息，以后上牌照，不再含有不吉利的数字了，这样一来，就可以消除个别的士司机和乘客的心理障碍，更安全地服务大众。
不吉利的数字为所有含有4或62的号码。例如：
62315 73418 88914
都属于不吉利号码。但是，61152虽然含有6和2，但不是62连号，所以不属于不吉利数字之列。
你的任务是，对于每次给出的一个牌照区间号，推断出交管局今次又要实际上给多少辆新的士车上牌照了。

Input

输入的都是整数对n、m（0<n≤m<1000000），如果遇到都是0的整数对，则输入结束。

Output

对于每个整数对，输出一个不含有不吉利数字的统计个数，该数值占一行位置。

Sample Input

1 100
0 0

Sample Output

80

 

来一道非常经典的数位dp,这道题也包含了许多数位dp的常用方法：拆位+记忆化搜索+判断封顶

具体的就不多说了···直接看代码吧

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int f[N][N][],a,b,num[N],n,ans1,ans2;
inline int R()
{
  char c;int f=;
  for(c=getchar();c<''||c>'';c=getchar());
  for(;c<=''&&c>='';c=getchar())
    f=(f<<)+(f<<)+c-'';
  return f;
}
inline void trans(int x)
{
  memset(f,-,sizeof(f));
  int temp=x;n=;
  while(temp)  n++,temp/=;
  temp=x;
  for(int i=n;i;i--)
    num[i]=temp%,temp/=;
}
inline int dfs(int pos,int pre,bool jud)
{
  if(pos==n+)  return ;
  if(f[pos][pre][jud]!=-)  return f[pos][pre][jud];
  int maxx=jud?num[pos]:,ans=;
  for(int i=;i<=maxx;i++)
  {
    if(i==||(pre==&&i==))  continue;
    ans+=dfs(pos+,i,jud&&i==maxx);
  }
  return f[pos][pre][jud]=ans;
}
int main()
{
  while(true)
  {
    a=R(),b=R();
    if(a==&&b==)  break;
    trans(a-);ans1=dfs(,,);
    trans(b);ans2=dfs(,,);
    cout<<ans2-ans1<<endl;
  }
  return ;
}

3.B-number（hdu3652）

Problem Description

A wqb-number, or B-number for short, is a non-negative integer whose decimal form contains the sub- string "13" and can be divided by 13. For example, 130 and 2613 are wqb-numbers, but 143 and 2639 are not. Your task is to calculate how many wqb-numbers from 1 to n for a given integer n.

Input

Process till EOF. In each line, there is one positive integer n(1 <= n <= 1000000000).

Output

Print each answer in a single line.

Sample Input

13 100 200 1000

Sample Output

1 1 2 2

和上道题很像啊···只是需要在dfs时多加入一个mod和一个jud来判断是否整除和是否找到13即可·······

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int f[N][N][][][N],num[N],n,a;
inline void trans(int x)
{
  memset(f,-,sizeof(f));
  int temp=x;n=;
  while(temp)  temp/=,n++;
  temp=x;
  for(int i=n;i>=;i--)  num[i]=temp%,temp/=;
}
inline int dfs(int pos,int mod,int jud,int lim,int pre)
{
  if(pos==n+)  return jud&&!mod;
  if(f[pos][mod][jud][lim][pre]!=-)  return f[pos][mod][jud][lim][pre];
  int maxx=lim?num[pos]:,ans=,vmod,vjud;
  for(int i=;i<=maxx;i++)
  {
    vmod=(mod*+i)%;vjud=jud;
    if(pre==&&i==)  vjud=;
    ans+=dfs(pos+,vmod,vjud,lim&&i==maxx,i);
  }
  return f[pos][mod][jud][lim][pre]=ans;
}
int main()
{
  //freopen("a.in","r",stdin);
  while(scanf("%d",&a)!=EOF)
  {
    trans(a);
    printf("%d\n",dfs(,,,,));
  }
  return ;
}

4.beautiful number（codeforces 55d）

题目描述

如果一个数能够被其每个除0的数位的数都整除，那么这个数就叫做美丽数。
给定一个区间 [x,y] ，计算该区间内有多少个美丽数。

输入格式

输入文件中有一行，为空格隔开的两个正整数 x 和 y（1≤x≤y≤9*1018）。

输出格式

输出一个整数，即区间 [x,y] 内的美丽数个数。

样例数据 1

输入　

1 9

输出

9

样例数据 2

输入　

12 15

输出

2

 

这道题首先先到的是用四维dp，第一维记录位数，第二维记录之前数的公倍数，第三维记录目前凑成的数的数字之和，最后一维记录是否封顶····

然而第二维和第三维是在太大···直接记录会超空间···

第三维其实是很好优化的···因为1到9的公倍数只有2520，因此每次之和模掉一个2520就可以了··

至于第二维···由于1到9各个数字组成的数的公倍数最多只有48个·····因此可以利用hash表来储存····（其实也不叫hash表··只是一个普通数组而已）

然后就可以了···另外注意要开long long啊···

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int num[N],n,tot,hash[],id[];
long long dp[N][][][],x,y,ans1,ans2;
inline void pre()
{
  for(int i=;i<=;i++)
    if(!(%i))  hash[++tot]=i,id[i]=tot;
}
inline void trans(long long x)
{
  memset(dp,-,sizeof(dp));
  long long temp=x;n=;
  while(temp)  n++,temp/=;
  temp=x;
  for(int i=n;i>=;i--)  num[i]=temp%,temp/=;
}
inline int gcd(int a,int b)
{
  if(b==)  return a;
  else return gcd(b,a%b);
}
inline int getlcm(int a,int b)
{
  return a*b/gcd(a,b);
}
inline long long dfs(int pos,int gbs,int mod,int lim)
{
  if(pos==n+)  return mod%hash[gbs]==;
  if(dp[pos][gbs][mod][lim]!=-)  return dp[pos][gbs][mod][lim];
  int maxx=lim?num[pos]:;int vgbs,vmod;long long ans=;
  for(int i=;i<=maxx;i++)
  {
    vmod=(mod*+i)%;vgbs=gbs;
    if(i)
    {
      vgbs=getlcm(i,hash[gbs]);vgbs=id[vgbs];
    }
    ans+=dfs(pos+,vgbs,vmod,lim&&i==maxx);
  }
  return dp[pos][gbs][mod][lim]=ans;
}
int main()
{
 // freopen("a.in","r",stdin);
  pre();
  scanf("%I64d%I64d",&x,&y);
  trans(y);ans1=dfs(,,,);
  trans(x-);ans2=dfs(,,,);
  printf("%I64d",ans1-ans2);
  return ;
}