UVA10689 Yet another Number Sequence —— 斐波那契、矩阵快速幂

题目链接：https://vjudge.net/problem/UVA-10689

题解：

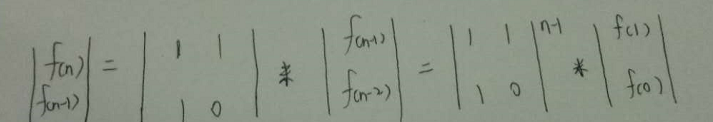
代码如下：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <cmath>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 using namespace std;
 typedef long long LL;
 const int INF = 2e9;
 const LL LNF = 9e18;
 //const int MOD = 1e9+7;
 const int MAXN = 1e6+;

 LL MOD;
 const int Size = ;
 struct MA
 {
     LL mat[Size][Size];
     void init()
     {
         for(int i = ; i<Size; i++)
         for(int j = ; j<Size; j++)
             mat[i][j] = (i==j);
     }
 };

 MA mul(MA x, MA y)
 {
     MA ret;
     memset(ret.mat, , sizeof(ret.mat));
     for(int i = ; i<Size; i++)
     for(int j = ; j<Size; j++)
     for(int k = ; k<Size; k++)
         ret.mat[i][j] += (1LL*x.mat[i][k]*y.mat[k][j])%MOD, ret.mat[i][j] %= MOD;
     return ret;
 }

 MA qpow(MA x, LL y)
 {
     MA s;
     s.init();
     while(y)
     {
         if(y&) s = mul(s, x);
         x = mul(x, x);
         y >>= ;
     }
     return s;
 }

 MA tmp = {
     , ,
     ,
 };

 int main()
 {
     LL f[], n, m;
     int T;
     scanf("%d", &T);
     while(T--)
     {
         scanf("%lld%lld%lld%lld",&f[],&f[],&n,&m);
         if(n<)
         {
             printf("%lld\n", f[n]);
             continue;
         }

         MOD = ;
         while(m--) MOD *= ;
         MA s = tmp;
         s = qpow(s, n-);
         LL ans = (1LL*s.mat[][]*f[]%MOD+1LL*s.mat[][]*f[]%MOD)%MOD;
         printf("%lld\n", ans);
     }
 }