我要好offer之 概率题大总结

1. 利用等概率Rand5生成等概率Rand3

Rand5生成等概率Rand3

这个题目可以扩展为：利用等概率RandM生成等概率RandN (M > N)

这里，我们首先明白一个简单的知识点：如果 randN 可以等概率生成 [0, N) 之间的数

假设 N = T的整倍数，那么我们可以直接使用 RandN() / (N / T) 来等概率生成 [0, T)之间的数

比如说，Rand21可以等概率生成[0, 21)之间的数，那么 Rand21() / 3 就可以等概率生成 [0, 7)之间的数，即 实现了 Rand7函数

// 利用 Rand5 实现 Rand3
int Rand3() {
    int tmp = Rand5();
    while (tmp >= ) {
        tmp = Rand5();
    }
    return tmp;
}

证明：以输出0为例，看看概率是多少。

x的第一个有效数值是通过Rand5得到的。Rand5返回0的概率是1/5，如果这事儿发生了，我们就得到了0，否则只有当Rand5返回3或4的时候，我们才有机会再次调用它来得到新的数据。

第二次调用Rand5之后，又是有1/5的概率得到0，2/5的概率得到3或4导致循环继续执行下去，如此反复。

因此概率的计算公式为：

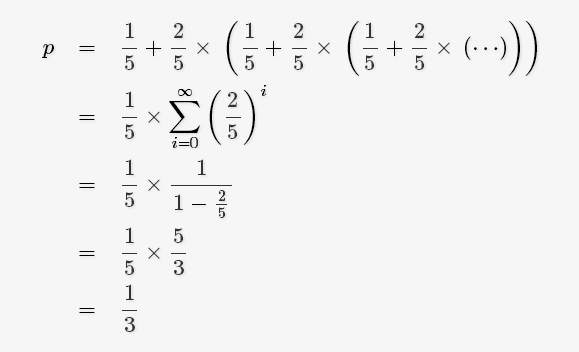
优化一下：我们在开始就说明了一个常识，这里，如果RandM 等概率 生成 RandN 时，当 M 很大 而 N 很小时，这时很多情况是在while里循环，可能一直循环

因此，我么把while循环的边界调整一下

int RandN() {
    int t = N;  // t是小于M的，N的最大倍数
    while (t + N < M) {
        t = t + N;
    }
    int tmp = RandM();
    while (tmp >= t) {
        tmp = RandM();
    }
    return tmp / (t / N);
}

2. 利用等概率Rand3生成等概率Rand5

Rand3生成等概率Rand5

这个题目可以扩展为：利用等概率RandM生成等概率RandN (M < N)

这里，我们要首先 说明一个知识点：

我们可以利用 等概率RandM函数 生成 等概率 Rand(M * M)

比如说：M = 5

step1. Rand5 可以等概率生成 , , , ,  (/5概率)

step2. 设 上一步Rand5的结果为t，则 mul = M * t 等概率生成：，，，， (/5概率)

step3. 再次调用 Rand5 等概率生成 , , , ,  ，设结果为 s (/5概率)
step4. 将step2 和 step3的两个结果相加， 就可以等概率生成 ，，... (相乘事件，/25概率)

这样就实现了 Rand25

因为这一题中M < N, 而我们可以直接利用 RandM 来 等概率生成 Rand(M * M) ，这时 M * M 很可能就大于N了，如果不大于N，那么再次 翻倍即可

假设 M * M 大于 N，联想到第一题，相信大家很容易给出第二题的解了

int RandN() {
    int t = N;  // t是小于M×M的，N的最大倍数
    while (t + N < M * M) {
        t = t + N;
    }
    int tmp = RandM() * M + RandM();  // 等概率生成 Rand(M*M)
    while (tmp >= t) {
        tmp = RandM();
    }
    return tmp;
}

3. 单次遍历，等概率随机选取1个

(未知行数文件的一行文本/未知长度单链表的一个结点)

等概率随机选取1个

问题描述：假设我们有一堆数据（可能在一个单链表里，也可能在文件里），数量未知。

要求只遍历一次这些数据，随机选取其中的一个元素，任何一个元素被选到的概率相等。

O(n)时间，O(1)辅助空间（n是数据总数，但事先不知道）

解题思路：如果元素总数为n，那么每个元素被选到的概率应该是1/n。然而n只有在遍历结束的时候才能知道，在遍历的过程中，n的值还不知道，可以利用乘法规则来逐渐凑出这个概率值

void GetRandomSingleLine(FILE* fp, char* randomLine) {
    srand(time(NULL));
    int i = ;
    char tmp[MAX_LINE];
    while (fgets(tmp, sizeof(tmp), fp) != NULL) {
        if (rand() % i == ) {   // rand() % i == 0 的概率为 1/i
            strcpy(randomLine, tmp);
        }
        ++i;
    }
}

当文件行数为1时，rand() % 1肯定为0，直接输出

当文件行数为2时，rand() % 2 等于0 的概率为 1/2，此时 输出第一行 和 第二行 的概率均为 1/ 2

当文件行数为3时：

输出第一行的概率是：1 * (1 - 1/2) * (1 - 1/3) = 1/3

输出第二行的概率是：1 * (1/2) * (1 - 1/3) = 1/3

输出第三行的概率是：1 - （1/3 + 1/3） = 1/3 (注意：题目要求必须输出一行)

4. 单次遍历，等概率随机选取k个：蓄水池抽样问题

(未知行数文件的K行文本/未知长度单链表的K个结点)

等概率随机选取k个(蓄水池抽样)

解题思路：先读入第 1 ~ k 行保存，以后每次读入第 i 行，都以 k / i 的概率把刚读入的一行随机替换之前保存的 k 行中的一行。

void GetRandomLines(FILE* fp, char** randomLine, int k) {
    srand(time(NULL));

    char tmp[MAX_LINE];
    // 读入文件第1到k行
    for (int i = ; i < k; ++i) {
        fgets(randomLine[i], MAX_LINE, fp);
    }

    int i = k + ;
    while (fgets(tmp, MAX_LINE, fp) != NULL) {
        if (rand() % i < k) {
            // 随机替换已有的某一行
            int j = rand() % k;
            strcpy(randomLine[j], tmp);
        }
        ++i;
    }
}

5. 等概率随机排列数组(随机洗牌 std::random_shuffle)

随机洗牌

问题描述：假设有一个数组，包含n个元素。现在要重新排列这些元素，要求每个元素被放到任何一个位置的概率都相等（即1/n），

并且直接在数组上重排（in place），不要生成新的数组。用O(n) 时间、O(1)辅助空间。

解题思路：

先想想如果可以开辟另外一块长度为n的辅助空间时该怎么处理，显然只要对n个元素做n次（不放回的）随机抽取就可以了。

先从n个元素中任选一个，放入新空间的第一个位置，然后再从剩下的n-1个元素中任选一个，放入第二个位置，依此类推。

按照同样的方法，但这次不开辟新的存储空间。第一次被选中的元素就要放入这个数组的第一个位置，但这个位置原来已经有别的（也可能就是这个）元素了，这时候只要把原来的元素跟被选中的元素互换一下就可以了。很容易就避免了辅助空间。

void Random(std::vector<int>& num) {
    srand(time(NULL));
    for (int i = num.size() - ; i >= ; --i) {
        int pos = rand() % (i + 1);
        std::swap(num.at(i), num.at(pos));
    }
}

6. 利用不均匀硬币产生等概率

利用不均匀硬币产生等概率

问题描述：有一枚不均匀的硬币，已知抛出此硬币后，正面向上的概率为p（ < p < ）。请利用这枚硬币产生出概率相等的两个事件

某一次抛出硬币，正面向上的概率是p，反面向上的概率是1 - p，当p不等于0.5时，这两个事件的概率就不一样了。

怎么能凑出等概率呢？还是要利用概率的加法和乘法法则。这里用乘法，也就是连续的独立事件。

连续抛两次硬币，正反面的出现有四种情况，概率依次为：

两次均为正面：p * p
第一次正面，第二次反面：p * ( - p)
第一次反面，第二次正面：( - p) * p
两次均为反面：( - p) * ( - p)

中间两种情况的概率是完全一样的。于是问题的解法就是连续抛两次硬币，如果两次得到的相同则重新抛两次；

否则根据第一次（或第二次）的正面反面情况，就可以得到两个概率相等的事件

扩展：

这一题实质就是 利用不均匀概率事件 生成 [0,1]之间的随机数

如何利用 不均匀概率事件 生活[0,n)之间的随机数呢？(即0，1，2... n-1这n个数)

我们每一轮都是连续抛n次硬币

每一轮中 正面出现次数为i，则反面出现次数为 n-i，相应概率为 C(n, i) * (Pⁱ) * (1-p)^(n-i)

当i=1或者n-1时，上述概率分别为 n*p*(1-p)^(n-1) 和 n*p^(n-1)*(1-p)

注意到上面2个概率的系数都是n，我们现在需要随机生成n个数，我们就可以将这两点联系起来

例如i=1，对应n种情况，我们将这n种情况对应编号 n个数

对于每一轮中正面出现次数不是1的时候，就重新再抛一轮